Remarks
본 포스팅은 Hands-On Machine Learning with Scikit-Learn & TensorFlow (Auérlien Géron, 박해선(역), 한빛미디어) 를 기반으로 작성되었습니다.
I. Linear regression
1. Hypothesis model
$\hat{y} = \theta_0 + \theta_1 x_1 + \cdots + \theta_n x_n = h_\theta(\mathbf{x}) = \theta^T \bf{x}$
- $\bf{x}$: feature vector
- $\theta$: parameter
- $n$: feature의 개수
2. Cost function
$MSE(X, h_\theta) = MSE(\theta) = \frac{1}{m}\sum_{i=1}^m(\hat{y}^{(i)} - y^{(i)})^2 = \frac{1}{m}\sum_{i=1}^m(\mathbf{x^{(i)}}^T \theta - y^{(i)})^2 $
- $m$: feature vector의 개수
3. Normal equation
Normal equation
해석적인 (analytic) 방법으로 cost function을 최소화시키는 parameter의 방정식입니다.
$\hat{\theta} = (X^TX)^{-1}X^T\bf{y}$
- Computational complexity
- $X^TX = [n+1, m] \cdot [m, n+1] = O(m(n+1)^2)$
- $(X^TX)^{-1} = [n+1, n+1] = O((n+1)^3)$
- $(X^TX)^{-1}X^T = [n+1, n+1] \cdot [n+1, m] = O(m(n+1)^2)$
- $(X^TX)^{-1}X^T\mathbf{y} = [n+1, m] \cdot [m, 1] = O(m(n+1))$ $\therefore \ O(n^3) + O(mn^2) = O(mn^2) \ (∵ m > n)$
그러나 sklearn에 구현된 LinearRegression은 $O(m^{0.72}n^{1.3})$ 정도의 복잡도를 가집니다. 1
4. Gradient Descent
Gradient descent
Cost function을 최소화시키기 위해 parameter에 대한 cost function의 gradient ($\nabla_\theta J(\theta)$)의 역방향으로 반복적으로 parameter를 이동시키는 방법입니다. 여러 종류의 문제에서 최적의 해법을 찾을 수 있어 범용적으로 사용할 수 있는 수치적인 (numerical) 최적화 알고리즘입니다. Feature의 개수에 민감하지 않다는 장점이 있습니다. (Complexity = $O(mn)$ per 1 step)
Linear regression (뿐만 아니라 polynomial regression2)의 cost function은 이차 초곡면 (quadric)3 중에서도 포물면 (paraboloid) 형태의 convex function이기 때문에 적절한 learning rate를 사용하면 gradient descent가 global minima에 가깝게 이동한다는 것이 보장되어 있습니다.
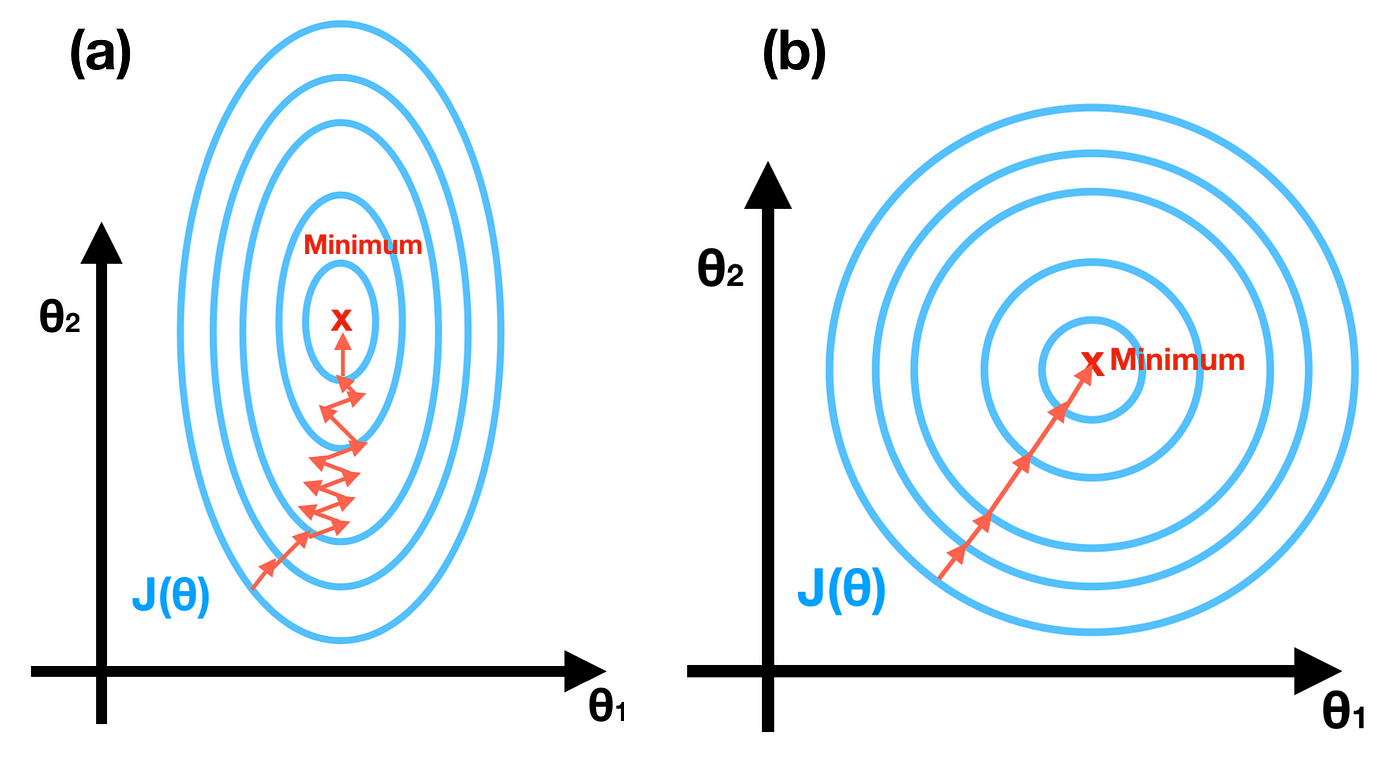
Gradient descent를 사용하기 전에는 반드시 각 feature의 scale이 동일하도록 만들어야 합니다.
모든 feature의 scale이 동일하지 않다면 비효율적인 궤적을 그리며 수렴하는 데 많은 시간이 소모되기 때문에, StandardScaler, normalize 등을 통해 모든 feature가 동일한 scale을 갖도록 만드는 것이 좋습니다.
$ \frac{\partial}{\partial \theta_j} J(\mathbf{\theta}) = \frac{2}{m} \sum_{i=1}^m(\mathbf{x^{(i)}}^T \theta - y^{(i)}) x^{(i)}_j $
$\theta_j$에 대한 편도함수에 $x_j^{(i)}$가 곱해져 있기 때문에 $\mathbf{x}_j$의 scale이 다른 feature와 차이가 날수록 수렴속도 또한 차이가 나게됩니다.
1) Batch Gradient Descent
Batch gradient descent
Parameter를 이동시키는 매 step 마다 전체 train data를 사용하여 $\nabla_\theta J(\theta)$ 를 계산하는 gradient descent 방법을 batch gradient descent라고 합니다.
- Complexity
$ \nabla_\theta J(\theta) = \frac{2}{m} X^T(X\theta - \mathbf{y}) $
- $ X\theta = [m, n+1] \cdot [n+1, 1] = O(m(n+1)) $
- $ X\theta - \mathbf{y} = [m, 1] - [m, 1] = O(m) $
- $ \frac{2}{m} X^T(X\theta - \mathbf{y}) = [n+1, m] \cdot [m, 1] = O(m(n+1)) $
$\therefore \ O(mn) $
사용되는 데이터의 개수($m$)가 많을수록 gradient를 계산하는데 걸리는 시간이 길어집니다.
- Hyperparameter (learning rate) tuning
적절한 learning rate를 찾기 위해 마찬가지로 grid search 혹은 random search를 사용할 수 있습니다.
수렴하는데 너무 많은 시간이 걸리는 모델을 막기 위해 반복 횟수를 제한해야 합니다.
주로 사용하는 방법은 반복 횟수를 크게 지정하고, gradient의 norm이 허용오차 (tolerance, $\epsilon$) 보다 작아지면 minima에 도달한 것으로 간주하여 알고리즘을 중지하는 것입니다.
2) Stochastic Gradient Descent
Batch gradient descent의 가장 큰 문제점은 매 step 마다 전체 train data를 사용하기 때문에 train data가 커지면 굉장히 느려지게 됩니다.
Stochastic gradient descent
매 step에서 단 1개의 데이터를 무작위로(stochastic) 선택하여 gradient를 계산하는 gradient descent 방법입니다.
Gradient를 계산하는 복잡도는 $O(n)$ 으로 줄어들기 때문에 굉장히 빠르게 학습되고 외부 메모리 학습 알고리즘으로 구현이 가능하다는 장점이 있지만, minima에 다다를 때까지 요동치며 평균적으로 감소하는 궤적을 그리게 됩니다.
또한, 알고리즘이 멈추었을 때 최적치라는 보장을 할 수 없습니다.
그러나, cost function이 굴곡이 많을 경우 이 무작위성 (stochasticity)은 local minima를 건너뛸 수 있도록 해주기 때문에 batch gradient descent 방법보다 global minima를 찾을 가능성이 더 높습니다.
- Learning schedule
매 step에서 learning rate를 결정하는 함수를 learning schedule이라 부릅니다.
Stochastic gradient descent의 무작위성을 통해 local minima를 탈출할 수 있고 global minima에 수렴할 수 있게 하기 위한 방법으로 큰 learning rate로 학습을 시작하고 점진적으로 감소시키는 learning schedule을 사용할 수 있습니다.
$\eta^{(t)} = \frac{\eta_0}{t^p}$ (hyperparameter: $\eta_0, p$) 와 같은 함수를 사용할 수 있습니다.
3) Mini-batch Gradient Descent
Mini-batch Gradient Descent
Mini-batch라 부르는 임의의 작은 sample set을 무작위로 (stochastic) 선택하여 gradient를 계산하는 방법입니다. Batch gradient descent와 stochastic gradient descent가 가지는 성질의 중간 위치에 있으며, GPU를 사용한 병렬처리에 가장 잘 최적화되어있습니다.
Batch gradient descent, stochastic gradient descent와 비교하여 다음과 같은 장점들이 있습니다.
- Batch gradient descent 에 비해
GPU를 최대한 활용할 수 있고 gradient 계산이 빠르다. ($O(m’n)$)
Local minima에서 빠져나가기 더 쉽다.
- Stochastic gradient descent 에 비해
Parameter space에서 덜 불규칙하게 움직인다.
Minima에 더 가까이 도달하게 된다.
Mini-batch gradient descent도 stochastic gradient descent와 마찬가지로 적절한 learning schedule을 사용하여야 합니다.
-
https://www.thekerneltrip.com/machine/learning/computational-complexity-learning-algorithms/ ↩
-
https://medium.com/100-shades-of-machine-learning/linear-regression-a-tale-of-a-transform-7e050cddbf17 ↩
-
https://ko.wikipedia.org/wiki/%EC%9D%B4%EC%B0%A8%EC%B4%88%EA%B3%A1%EB%A9%B4 ↩
-
https://www.coursera.org/learn/machine-learning?source=post_page————————— ↩