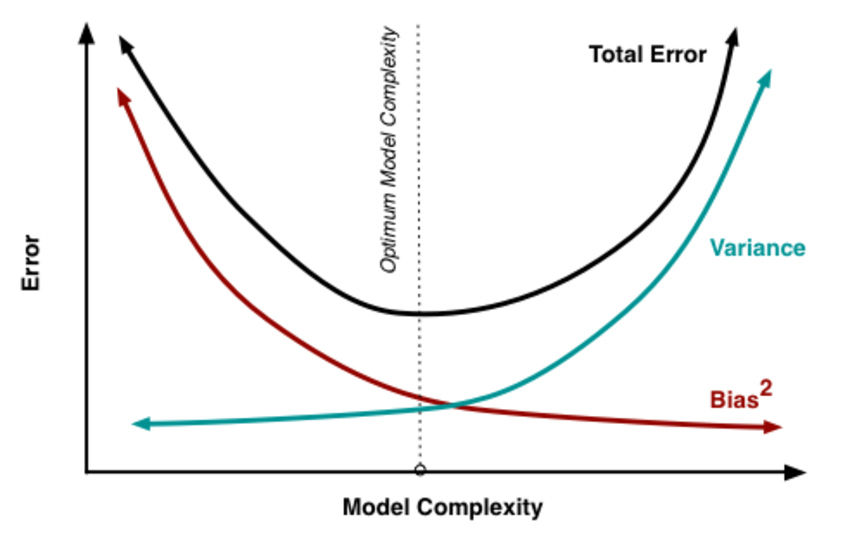
Bias-variance trade-off
모델의 일반화 오차는 모델의 $Bias^2$와 $Variance$과 데이터의 $noise$의 합으로 표현된다.
Remarks
본 포스팅은 https://www.datacamp.com/community/tutorials/tutorial-ridge-lasso-elastic-net 을 참고하여 작성되었습니다.
1. 데이터 X와 Y가 어떠한 target function (true function) $f(X)$와 noise $\epsilon$에 대하여, $Y = f(X) + \epsilon$ 의 관계를 가진다고 가정합니다.
\(\begin{align}
f(X) &: \text{target function} \\
\hat{f}(X) &: \text{estimator} \\
\bar{f}(X) &: \text{expectation of } \hat{f}(X)
\end{align}\)
2. Target function을 구하기 위해 알고 있는 sample들(train data)로부터 target function를 추정해야합니다.
3. Estimator에 대해 고려해야할 2가지 중요한 성질로 bias와 variance가 있습니다.
- Bias
Target function과 estimator의 차이를 의미합니다.
단순화된(잘못된) 가정으로 인해 생긴 것으로, Estimate들의 accuracy를 나타냅니다.
예를 들어, 데이터가 실제로는 2차인데 선형으로 가정하는 경우 큰 bias를 가지게 되며 underfitting하기 쉽습니다. - Variance
Estimator의 분산을 의미합니다.
학습 데이터에 있는 작은 변동에 모델이 과도하게 민감하기 때문에 발생하는 것으로, estimate들의 spread 혹은 uncertainty를 측정합니다.
예를 들어, 자유도가 높은 모델(고차 다항 회귀 모델)은 높은 variance를 가지기 쉬워 overfitting되는 경향이 있습니다.
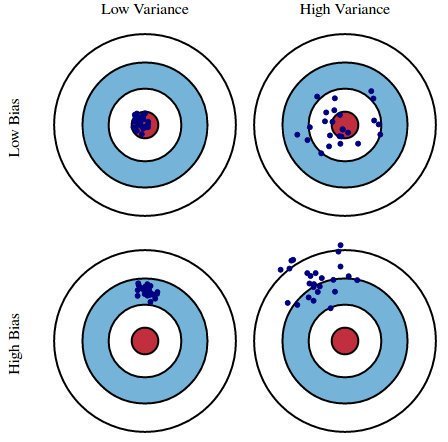
4. 다음은 4개의 다른 성질을 가진 estimator들로부터 나온 estimates를 파란색 shot으로 나타낸 그림입니다.
과녁 가운데 bull’s eye는 true population parameter를 나타냅니다.
5. 모델의 오차 (prediction error)는 이전에 살펴본 bias, variance, noise의 3가지로 나누어집니다.
\(\begin{equation}
\begin{split}
E(e) & = E[(Y - \hat{Y})^2] \\
& = E[(f(X) + \epsilon - \hat{f}(X))^2] \\
& = E[(f(X) - \hat{f}(X))^2 + \color{magenta}{\epsilon^2} + \color{green}{2\epsilon(f(X) - \hat{f}(X))]} \\
& = E[(f(X) - \hat{f}(X))^2] + \color{magenta}{\sigma^2} + \color{green}{0} \\
& = E[(f(X) - \bar{f}(X) + \bar{f}(X) - \hat{f}(X))^2] + \color{magenta}{\sigma^2} \quad \cdots \quad \text{let } \bar{f}(X) = E[\hat{f}(X)] \\
& = E[(f(X) - \bar{f}(X))^2] + E[(\hat{f}(X) - \bar{f}(X))^2] + E[2(f(X) - \bar{f}(X)) \color{green}{(\bar{f}(X) - \hat{f}(X))}] + \color{magenta}{\sigma^2} \\
& = \color{blue}{(f(X) - \bar{f}(X))^2} + \color{red}{E[(\hat{f}(X) - \bar{f}(X))^2]} + \color{magenta}{\sigma^2} \\
& = \color{blue}{Bias^2} \ + \ \color{red}{Variance} \ + \ \color{red}{irreducible \ error}
\end{split}
\end{equation}\)
6. Bias-variance trade-off
Model Complexity $\bf{\propto \frac{Variance}{Bias}}$
Feature들이 서로 많이 연관되어 있거나, feature의 개수가 sample의 개수와 비슷할 정도로 많으면 variance는 거의 무한대에 다다를 수 있습니다. 이를 해결하기 위해 약간의 bias를 추가하여 variance를 낮추는 방법을 사용할 수 있는데, 이러한 방법을 regularization이라고 합니다.
실제로 bias와 variance의 구체적인 값을 계산하여 확인할 수는 없지만, bias와 variance를 적절히 조절하여 total error가 가장 낮은 Optimum Model Complexity에 도달할 수 있도록 염두하고 있어야 합니다.