Learning curve

모델의 일반화 성능을 평가하기 위해 cross-validation이나 learning curve에 나타나는 training error와 validation error를 비교할 수 있습니다.

Remarks

본 포스팅은 Hands-On Machine Learning with Scikit-Learn & TensorFlow (Auérlien Géron, 박해선(역), 한빛미디어) 를 기반으로 작성되었습니다.

여기서는 learning curve를 살펴보겠습니다.
Learning curve는 X축이 train data의 크기, Y축이 error에 해당하는 곡선입니다.

2차 함수에서 100번 sampling한 데이터에 대한 예제입니다.
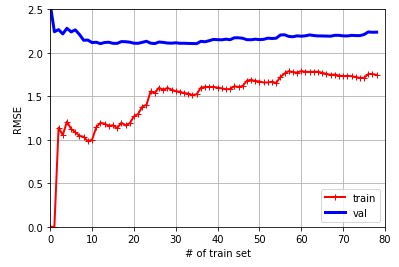
먼저 기본적인 linear regression에 대한 learning curve입니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

def plot_learning_curves(model, X, y):
  X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
  train_errors, val_errors = [], []

  for m in range(1, len(X_train)):
    model.fit(X_train[:m], y_train[:m])
    y_train_predict = model.predict(X_train[:m])
    y_val_predict = model.predict(X_val)

    train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
    val_errors.append(mean_squared_error(y_val, y_val_predict))

  plt.plot(np.sqrt(train_errors), 'r-+', lineqwidth=2, label='train')
  plt.plot(np.sqrt(val_errors), 'b-', linewidth=3, label='val')
  plt.xlabel('# of train set');  plt.ylabel('RMSE')
  plt.grid();  plt.legend()
  plt.axis([0, 80, 0, 2.5])
  plt.show()

lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)

10차 polynomial regression입니다.

1
2
3
4
5
6
7
8
from sklearn.pipeline import Pipeline

polynomial_regression = Pipeline([
    ('poly_features', PolynomialFeatures(degree=10, include_bias=False)),
    ('lin_reg', LinearRegression())
])

plot_learning_curves(polynomial_regression, X, y)

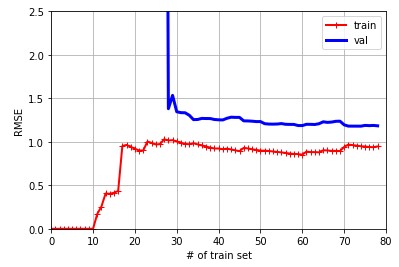
일반적으로 두 곡선이 수평한 공간을 만들고 꽤 높은 오차에서 매우 가까이 근접해 있는 경우, underfitting을 의심해봐야 합니다.

반면, 두 곡선 사이의 차이가 큰 경우 overfitting을 위험이 있으므로 반드시 확인해볼 필요가 있습니다.

PREVIOUSEtc