Confidence Interval

Remarks

표본을 사용하여 모수를 추정하는 경우, 모수가 어느 범위 안에 있는지 보여주는 방법을 신뢰구간(confidence interval)이라고 합니다.

예를 들어, 모평균 $\mu$에 대한 95% 신뢰구간의 의미에 대해서 살펴보도록 하겠습니다.

모평균 = $E[X] = \mu$, 모분산 = $Var[X] = \sigma^2$
표본의 크기 = $n$, 표본평균 = $\bar{X} = \frac{X_1 + \cdots + X_n}{n}$

표본평균 $\bar{X}$의 확률분포에서 $\mu$를 중심으로 생각해보면, 추출한 표본평균이 $[\mu - 1.96 * \sqrt{\frac{\sigma^2}{n}}, \ \mu + 1.96 * \sqrt{\frac{\sigma^2}{n}}]$ 의 범위에 있을 확률이 0.95 입니다. 이런 방식으로 모평균 $\mu$를 알고 있을 때 추출될 표본평균의 값을 예상할 수 있습니다.

그러나 반대로 우리는 알고 있는 표본평균으로부터 알지 못하는 모평균을 추정하려는 것이기 때문에 표본평균의 입장에서 모평균이 있을 범위(신뢰구간)를 다음과 같이 생각해보겠습니다.
$\bar{X}$가 $[\mu - 1.96 * \sqrt{\frac{\sigma^2}{n}}, \ \mu + 1.96 * \sqrt{\frac{\sigma^2}{n}}]$ 에 있을 확률이 95% 라는 말은,
$\mu$가 $[\bar{X} - 1.96 * \sqrt{\frac{\sigma^2}{n}}, \ \bar{X} + 1.96 * \sqrt{\frac{\sigma^2}{n}}]$ 에 있을 확률이 95% 라는 말과 대칭적으로 동일합니다.

여기서 주의해야할 점은, 신뢰구간이라는 개념은 frequentism에 기반한 것으로 모평균 $\mu$는 어떤 확률에 의해 값이 변하는 확률변수가 아니라 고정된 상수라는 것입니다.
즉, $\mu$는 표본평균($\bar{X_i}$)을 추출하고 신뢰구간($[\bar{X_i} - 1.96 * \sqrt{\frac{\sigma^2}{n}}, \ \bar{X_i} + 1.96 * \sqrt{\frac{\sigma^2}{n}}]$)을 생성하는 과정을 무한 번 반복($\lim\limits_{i \to \infty}$)했을 때 생성되는 수많은 신뢰구간들 중 $\mu$를 포함하는 신뢰구간의 상대도수가 95%에 수렴한다는 뜻으로 해석해야 합니다.

다음 그림은 95% 신뢰구간 100개를 생성하였을 때 모평균을 포함하는 신뢰구간이 96개로 대략 95%라는 것을 보여주고 있습니다.
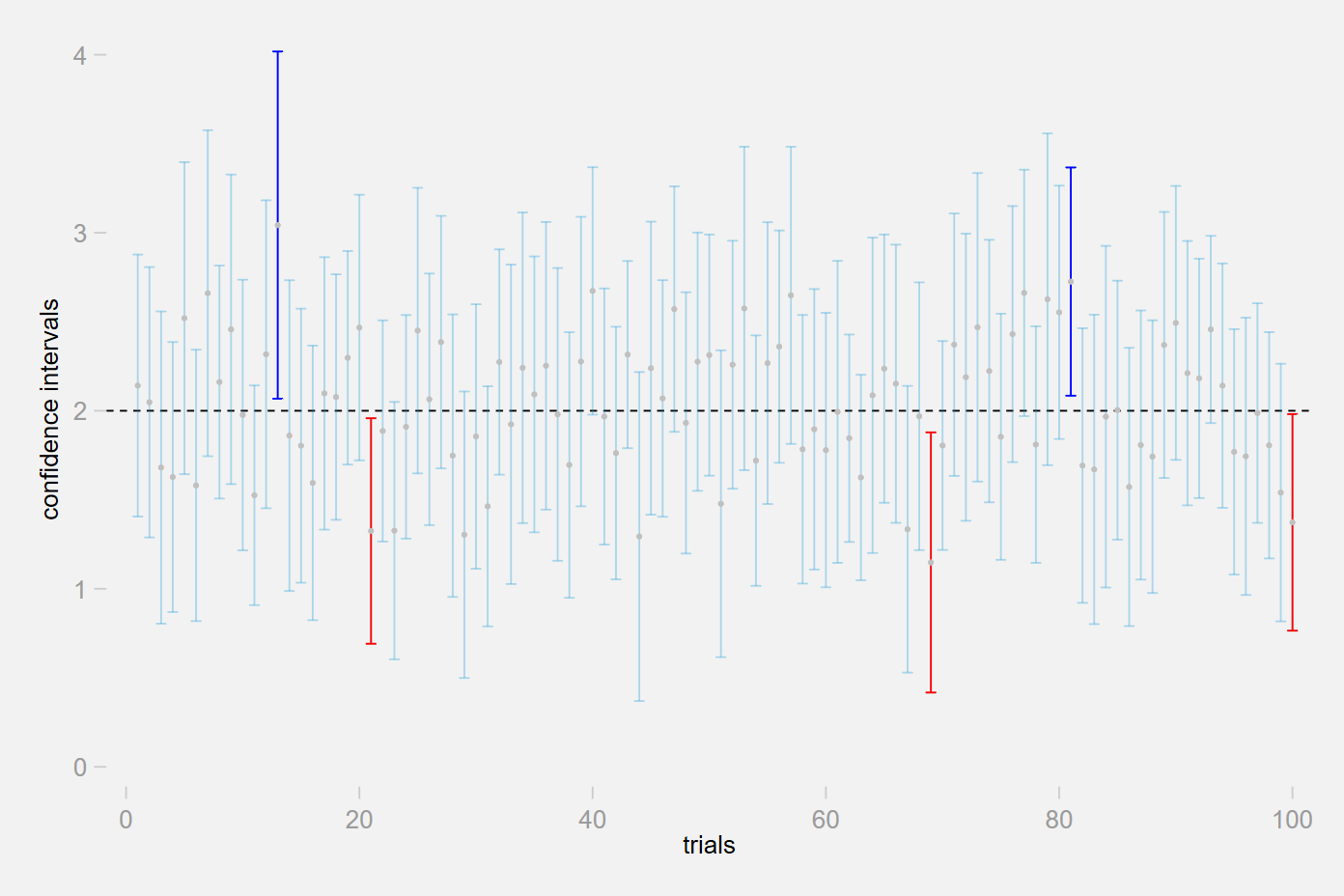Plot 출처: https://econbigdata.tistory.com/37

결국 단 한 번 $n$개의 표본을 추출하여 구한 $\mu$에 대한 95% 신뢰구간이 $[1.5, 2.1]$ 이라면, 이는 무한히 생성되는 신뢰구간 중 하나로써 $\mu$를 포함할 가능성이 95%가 된다는 것으로 해석할 수 있습니다.

PREVIOUSEtc