Remarks
이 글은 Computer Vision: Models, Learning, and Inference를 참고하여 작성되었습니다.
I. Motivation
1) MLE가 closed form solution으로 구해지기 위해선, (log) likelihood가 closed form으로 나와야하지만 그렇지 못한 경우가 많습니다.
2) 그러한 경우, hidden(latent) variable을 추가하는 방법을 사용하면 문제를 비교적 쉽게 풀 수 있습니다.
3) Hidden variable을 도입하여 MLE (혹은 MAP)를 구하는 알고리즘이 바로 EM algorithm입니다.
II. Algorithm
1. Likelihood with hidden variable $h$
\[\begin{equation} \begin{aligned} Pr(\mathbf{x} \mid \theta) &= \int Pr(\mathbf{x}, \mathbf{h} \mid \theta) d\mathbf{h} \\ &= \int Pr(\mathbf{x} \mid \mathbf{h}, \theta) Pr(\mathbf{h} \mid \theta) d\mathbf{h} \\ &= \int Pr(\mathbf{x} \mid \mathbf{h}, \theta) Pr(\mathbf{h}) d\mathbf{h} \quad \cdots \quad \mathbf{h} \text{ is independent to } \theta \end{aligned} \end{equation}\]2. Define a lower bound on log likelihood
\[\begin{equation} \begin{aligned} \log Pr(\mathbf{x} \mid \theta) &= \log \Pi_{i=1}^N Pr(x_i \mid \theta) \\ &= \Sigma_{i=1}^N \log Pr(x_i \mid \theta) \\ &= \Sigma_i \log \int Pr(x_i, h_i \mid \theta) dh_i \\ &= \Sigma_i \log \int q_i(h_i) \frac{Pr(x_i, h_i \mid \theta)}{q_i(h_i)} dh_i \\ &\geq \Sigma_i \int q_i(h_i) \log \frac{Pr(x_i, h_i \mid \theta)}{q_i(h_i)} dh_i \quad \cdots \quad \text{Jensen's inequality} \\ &= B[\{q_i(h_i)\}, \theta] \end{aligned} \end{equation}\]3. E-step (Expectation): Update the lower bound $B[{q_i(h_i)}, \theta]$ w.r.t. $q_i(h_i)$
Fix $\theta$ in E-step
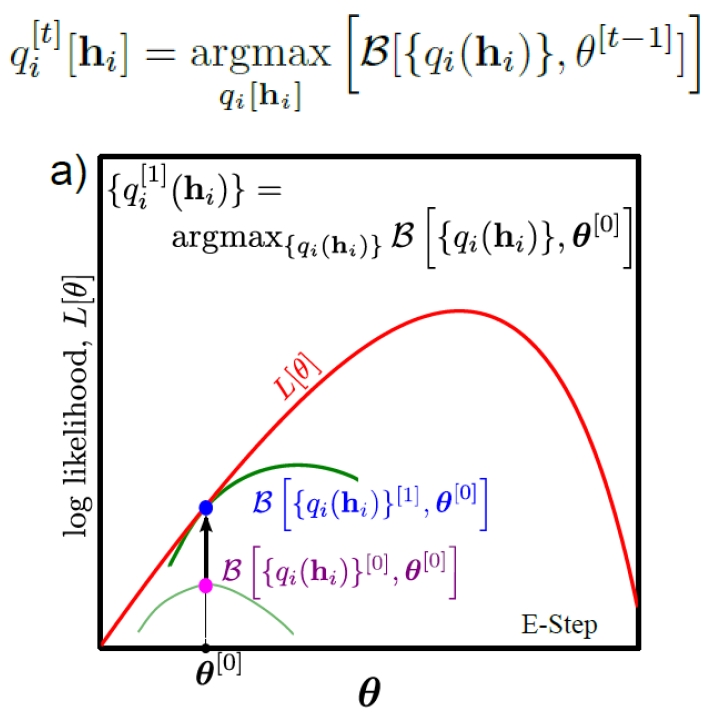
1) Express on $ B[{q_i(h_i)}, \theta] $
\[\begin{equation} \begin{aligned} B[\{q_i(h_i)\}, \theta] &= \Sigma_i \int q_i(h_i) \log \frac{Pr(x_i, h_i \mid \theta)}{q_i(h_i)} dh_i \\ &= \Sigma_i \int q_i(h_i) \log \frac{Pr(h_i \mid x_i, \theta) Pr(x_i \mid \theta)}{q_i(h_i)} dh_i \\ &= \Sigma_i \int q_i(h_i) [\log Pr(x_i \mid \theta) - \log \frac{q_i(h_i)}{Pr(h_i \mid x_i, \theta)}] dh_i \\ &= \Sigma_i \int q_i(h_i) \log Pr(x_i \mid \theta) dh_i - \Sigma_i \int q_i(h_i) \log \frac{q_i(h_i)}{Pr(h_i \mid x_i, \theta)} dh_i \\ &= \Sigma_i \log Pr(x_i \mid \theta) - \Sigma_i D_{KL}(q_i(h_i) \parallel Pr(h_i \mid x_i, \theta)) \\ \end{aligned} \end{equation}\]2) Optimize $q_i(h_i)$ on $ B[{q_i(h_i)}, \theta] $
\[\begin{equation} \begin{aligned} \hat{B}[\{q_i(h_i)\}, \theta] &= \text{argmax}_{q_i(h_i)}B[\{q_i(h_i)\}, \theta] \\ &= \text{argmax}_{q_i(h_i)} \Sigma_i \log Pr(x_i \mid \theta) - \Sigma_i D_{KL}(q_i(h_i) \parallel Pr(h_i \mid x_i, \theta)) \\ &= \text{argmax}_{q_i(h_i)} - \Sigma_i D_{KL}(q_i(h_i) \parallel Pr(h_i \mid x_i, \theta)) \\ &= \text{argmin}_{q_i(h_i)} \Sigma_i D_{KL}(q_i(h_i) \parallel Pr(h_i \mid x_i, \theta)) \\ \therefore \hat{q}_i(h_i) &= Pr(h_i \mid x_i, \theta) \end{aligned} \end{equation}\]3) Compute $Pr(h_i \mid x_i, \theta)$ using Bayes’ rule
$ Pr(h_i \mid x_i, \theta) = \frac{Pr(x_i \mid h_i, \theta) Pr(h_i)}{Pr(x_i \mid \theta)} $
4. M-step (Maximization): Maximize the lower bound $B[{q_i(h_i)}, \theta]$ w.r.t. parameters $\theta$
Fix ${q_i(h_i)}$ in M-step
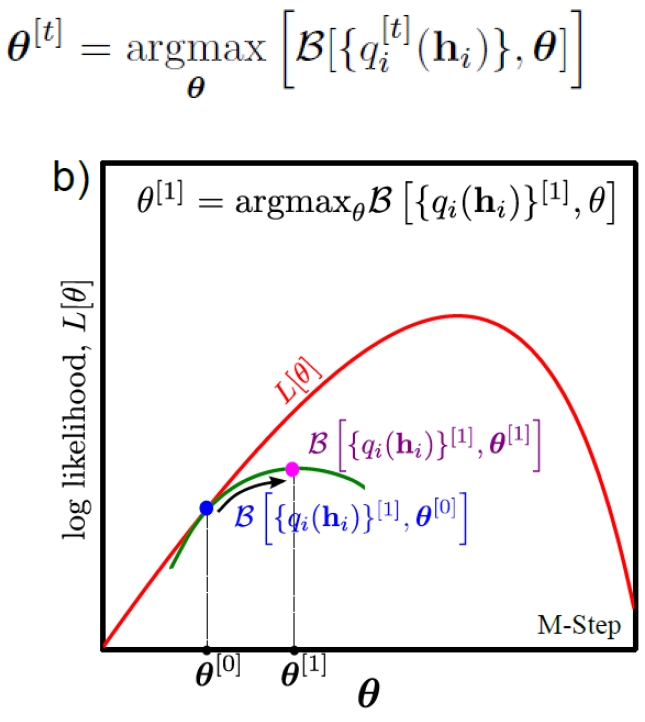
5. Iterate E-step & M-step: EM algorithm
$ \text{Iterate until the } \theta \text{ are converged} $
$ \quad \quad \mathbf{E-step: } \ \hat{q}_i(h_i) ← Pr(h_i \mid x_i, \theta^{(t)}) = \frac{Pr(x_i \mid h_i, \theta^{(t)}) Pr(h_i)}{Pr(x_i \mid \theta^{(t)})} $
$ \quad \quad \mathbf{M-step: } \ \hat{\theta}^{(t+1)} ← \text{argmax}_\theta \Sigma_i \int \hat{q}_i(h_i) \log Pr(x_i, h_i \mid \theta^{(t)}) dh_i$