Remarks

이 글은
CS231n
https://dalpo0814.tistory.com/29
등을 참고하여 작성되었습니다.

---

Notation

$W$: Weight vector
$L(W)$: Loss function with weight $W$
$\eta$: Learning rate(step size)
$\rho$: Friction rate
$\gamma, \beta_1, \beta_2$: Decay rate
$N$: number of data
$B$: batch size

0. Before using Gradient Descent

비효율적인 zigzag path(jittering)로 학습되는 것을 방지하기 위하여, 모든 feature의 scale을 동일하게 맞춰주어야한다.

1. (Batch) Gradient Descent (GD)

전체 데이터에 대하여 gradient를 계산하고 gradient descent를 수행한다.

• Algorithm (1 epoch)
  $W_{t+1} ← W_t - \eta \nabla L(W_t)$

2. Stochastic Gradient Descent (SGD)

학습시킬 때마다 sample(mini-batch)을 뽑아 gradient를 계산하고 gradient descent를 수행한다.

• Stochastic?
  전체 데이터에 대한 gradient를 계산해야하나, 실제로 사용하기엔 너무 계산량이 크다.
  그래서 적은 개수의 sample에 대한 sample gradient를 계산하여 full gradient를 추정하는 방식을 사용하게 되었는데,
  Monte Carlo method와 유사하기 때문에 stochastic 이라는 이름이 붙여졌다.
  

• Stop in local minima / saddle point
  Gradient = 0 인 지점에서 학습이 멈추는 문제점이 있다.

• Noise from sampling(mini-batch)
  Full gradient를 추정하는 과정에서 생기는 noise로 인해 최적의 학습을 하기 어렵다.

• Algorithm (1 epoch)
  while $N$ // $B$ iterations
    Sample mini-batch from data
    $W_{t+1} ← W_t - \eta \ \nabla L(W_t)$
  

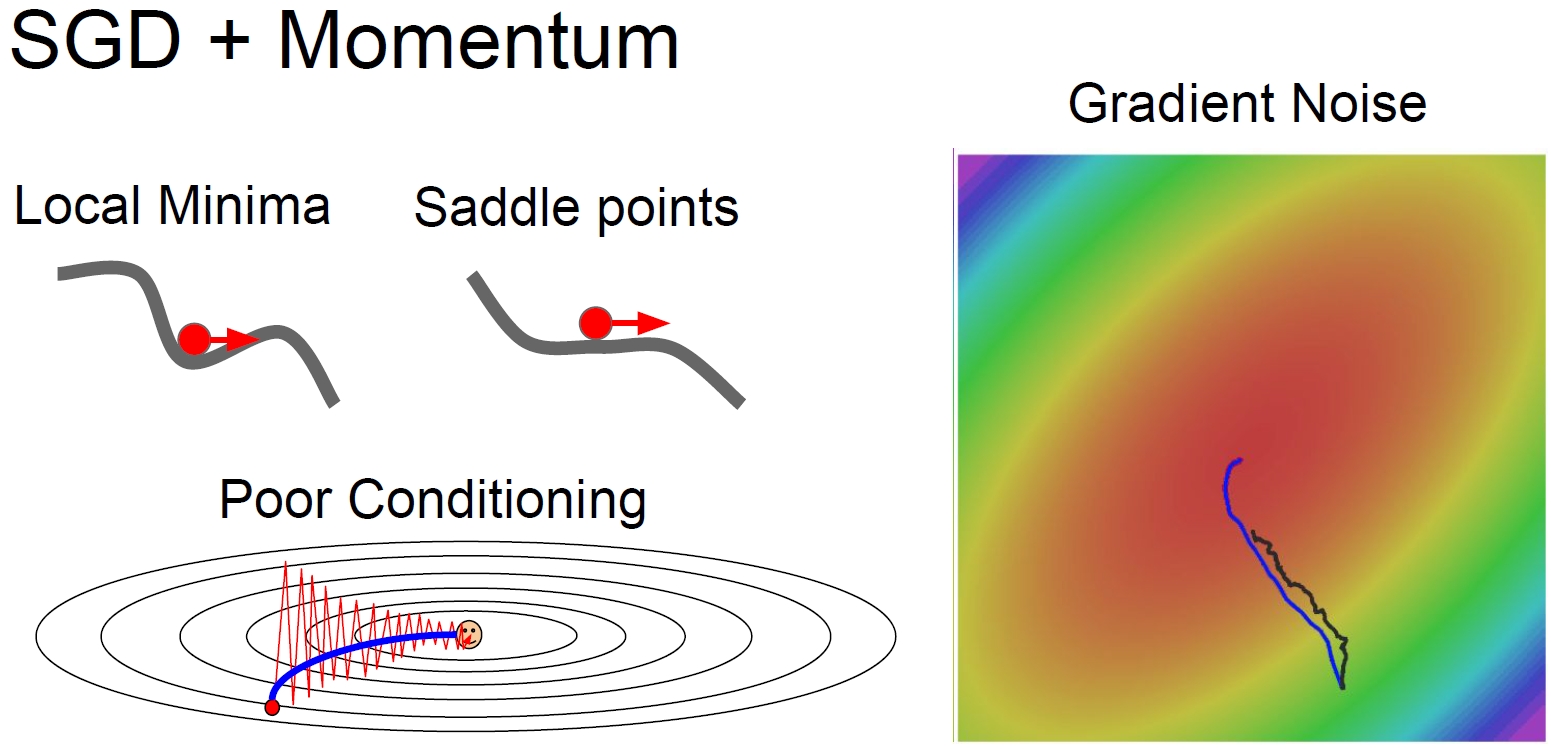
3. SGD with Momentum (Momentum SGD)

가속도(탄력)의 개념을 추가하여 속도에 gradient를 더한 값으로 gradient descent를 수행한다.

• SGD의 문제점들(poor conditioning, local minima/saddle point, gradient noise)을 해결하는데 도움이 된다.(velocity를 구할 때, 평균을 구하는 것처럼 noise를 경감시키는 효과가 있다)

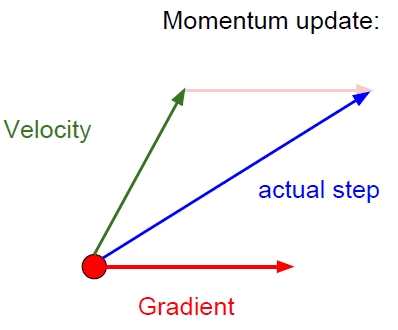
• 일반적으로 friction rate $\rho$를 0.9 혹은 0.99로 사용하고, velocity $v$의 초깃값으로 0를 사용한다.

• Algorithm (1 epoch)
  while $N$ // $B$ iterations
    Sample mini-batch from data
    $v_{t+1} ← \rho v_t + \nabla L(W_t)$
    $W_{t+1} ← W_t - \eta \ v_{t+1}$
  

4. SGD with Nesterov Momentum

현재 위치에서 gradient를 계산하는 momentum update와는 달리, velocity만으로 update한 지점에서 계산한 gradient를 사용하여 gradient descent를 수행한다.

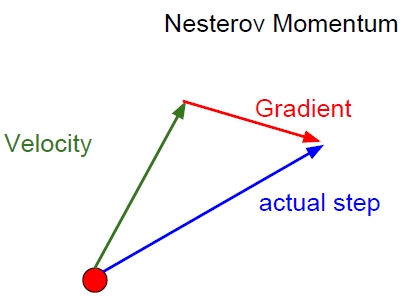
• Algorithm (1 epoch)
  while $N$ // $B$ iterations
    Sample mini-batch from data
    $v_{t+1} ← \rho v_t - \eta \ \nabla L(W_t + \rho v_t)$
    $W_{t+1} ← W_t + v_{t+1}$
  
  이 식을 다음과 같이 현재의 velocity와 과거의 velocity 간의 오류($v_{t+1} - v_t$: correction factor)를 수정하는 항목과의 결합으로도 생각할 수 있다.
  
  Let $\tilde{W_t} = W_t + \rho v_t$
  while $N$ // $B$ iterations
    Sample mini-batch from data
    $v_{t+1} ← \rho v_t - \eta \ \nabla L(\tilde{W_t})$
    $\tilde{W_{t+1}} ← \tilde{W_t} - \rho v_t + (1 + \rho) v_{t+1}$
          $\tilde{W_t} + v_{t+1} + \rho(v_{t+1} - v_t)$
  

5. AdaGrad

각각의 weight가 계산해온 gradient들에 대한 제곱합을 사용하는 방법이다.

• Gradient가 큰 경우 큰 값을 나누고, gradient가 작은 경우 작은 값을 나누어 적당한 크기만큼 update되도록 하는 방법이다.

• Convex function에 대해서는 효과적이지만 non-convex function에 대해서는 local minima / saddle point를 넘어갈 수 없다는 문제점이 있고 시간이 지날수록 gradient의 제곱합 $S$가 계속 증가하여 학습이 제대로 되지 않기 때문에 잘 사용하지 않는다.

• Algorithm (1 epoch)
  for each weight $w$
    $S_0 ← 0$
    while $N$ // $B$ iterations
     Sample mini-batch from data
     $g_{t+1} ← \frac{\partial L(w_t)}{\partial w}$
     $S_{t+1} ← S_t + g_{t+1}^2$
     $w_{t+1} ← w_t - \eta \ \frac{g_{t+1}}{\sqrt{S_{t+1}} + \epsilon}$
  

6. RMSProp

Gradient들의 제곱합을 사용하는 AdaGrad의 아이디어를 유지하면서 약간 변형된 알고리즘이다.

• Gradient의 제곱합 $S$가 계속 쌓이는 것이 아니라 time step이 지날수록 weight가 decay rate $\gamma$ 만큼 감쇠되도록 합을 계산하는 exponential moving average를 사용한다. 이는 결국 momentum update와 유사한 수행을 하게된다.
• Momentum의 경우 gradient가 overshooting되었다가 minima로 돌아오는 경향을 보이는 반면, RMSProp은 모든 feature에 대해 어느정도 균등한 수렴속도를 가지도록 조절한다.
• 그러나 여전히 local minima / saddle point에 안착하면 벗어날 수 없는 문제점이 있다.

• Decay rate $\gamma$로 0.9, $\epsilon$으로 $10^{-7}$ 정도의 값을 사용한다.

• Algorithm (1 epoch)
  for each weight $w$
    $S_0 ← 0$
    while $N$ // $B$ iterations
     Sample mini-batch from data
     $g_{t+1} ← \frac{\partial L(w_t)}{\partial w}$
     $S_{t+1} ← \gamma S_t + (1 - \gamma) g_{t+1}^2$
     $w_{t+1} ← w_t - \eta \ \frac{g_{t+1}}{\sqrt{S_{t+1}} + \epsilon}$
  

7. Adam

Momentum과 gradient의 제곱합을 사용하는 아이디어를 조합한 알고리즘이다.

• Momentum과 관련된 $m$과 gradient의 제곱합과 관련된 $v$ 두가지 moment를 사용하였고, bias를 제거하기 위해 $\hat{m}$과 $\hat{v}$로 만들어 최종적으로 update에 사용하였다.

• 알고리즘은 크게 2가지 부분으로 나누어져있다.
  2개의 moment를 weighted sum(exponential moving average)으로 계산
  First moment $E[g_{t+1}]$에 대한 moment estimate $m_{t+1}$(exponential moving average)를 계산($E[g_{t+1}] ≈ m_{t+1}$)
  Second moment $E[g_{t+1}^2]$에 대한 moment estimate $v_{t+1}$(exponential moving average)를 계산($E[g_{t+1}^2] ≈ v_{t+1}$)
  
  Bias를 보정
  $m_{t+1}$을 $1 - \beta_1^{t+1}$로 나누어 bias를 보정 $(E[g_{t+1}] = E[\hat{m_{t+1}}])$
  $v_{t+1}$을 $1 - \beta_2^{t+1}$로 나누어 bias를 보정 $(E[g_{t+1}^2] = E[\hat{v_{t+1}}])$
  이 과정을 통해 첫 time step에서 $\frac{\hat{m}_1}{\sqrt{\hat{v}_1} + \epsilon} = \frac{1 - \beta_1}{\sqrt{1 - \beta_2} + \epsilon}$ 의 값이 매우 커져서 overshooting되는 현상을 방지할 수도 있다.

• Decay rate $\beta_1$과 $\beta_2$는 각각 0.9, 0.999 정도의 값을 사용하고, learning rate $\eta$는 $10^{-3}, 5 \cdot 10^{-4}$ 정도의 값에서 잘 작동한다.\hat{m_{t+1}}

• Algorithm (1 epoch)
  for each weight $w$
    $m_0 ← 0$   (Initialize $1^{st}$ moment)
    $v_0 ← 0$   (Initialize $2^{nd}$ moment)
    while $N$ // $B$ iterations
     Sample mini-batch from data
     $g_{t+1} ← \frac{\partial L(w_t)}{\partial w}$          (Get gradient w.r.t. stochastic objective at timestep t+1)
     $m_{t+1} ← \beta_1 m_t + (1 - \beta_1) g_{t+1}$   (Update biased first moment estimate)
     $v_{t+1} ← \beta_2 v_t + (1 - \beta_2) g_{t+1}^2$    (Update biased second raw moment estimate)
     $\hat{m_{t+1}} ← \frac{m_{t+1}}{1 - \beta_1^{t+1}}$          (Compute bias-corrected first moment estimate)
     $\hat{v_{t+1}} ← \frac{v_{t+1}}{1 - \beta_2^{t+1}}$          (Compute bias-corrected second raw moment estimate)
     $w_{t+1} ← w_t - \eta \ \frac{\hat{m_{t+1}}}{\sqrt{\hat{v_{t+1}}} + \epsilon}$     (Update parameter)
  

8. Learning schedule

고정된 learning rate를 사용하는 대신, update 할수록 learning rate가 감소하는 방법을 사용할 수 있다.(learning rate 결정 후 decay rate 결정)

• Step decay: 몇 epoch 마다 절반으로 감소
  Exponential decay: $\eta = \eta_0 e^{-kt}$
  1/t decay: $\eta = \eta_0 / (1 + kt)$
  

• Momentum method와 같이 사용하는 것이 일반적이고 Adam과는 잘 쓰이지 않는다.