Remarks

본 글은 한양대학교 이기천 교수님의 시계열분석 강의 1강을 정리한 글입니다.

---

1. Time Series

1) Time Series

A time series is a realization of a sequence (time step) of random variables
Time series $\approx$ a stochastic process of $X_1, X_2, \cdots, X_t, \cdots$

2. White Noise

1) White noise

A stochastic process $a_0, a_1, \cdots$ is white noise if
the noise is $iid$ random variables with mean $0$ and constant variance $\sigma^2$
ex) $a_t \stackrel{iid}{\sim} N(0, \sigma^2)$

2) Notation

$a_t \sim WN(0, \sigma^2)$

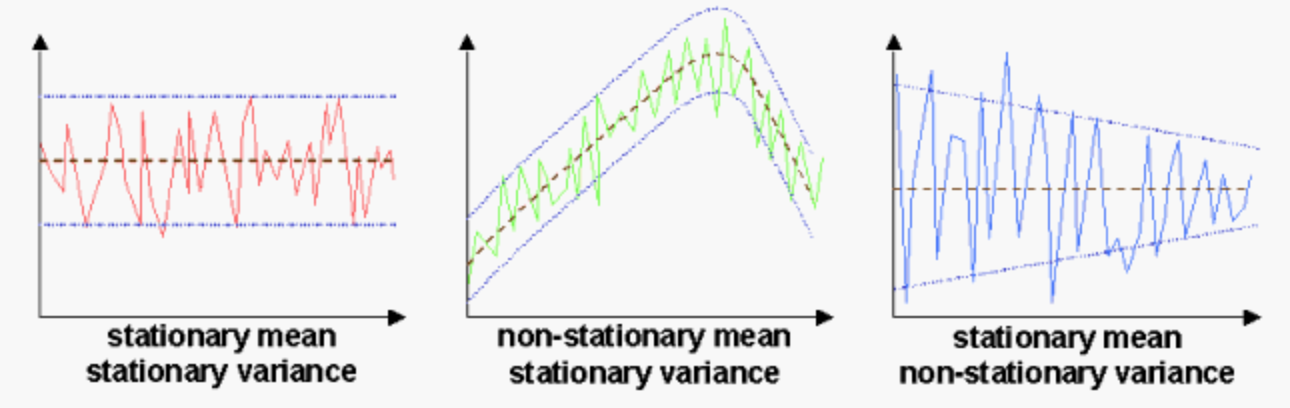
3. Stationary time Series

실제로는 2개 이상인 변수에 대한 결합분포를 분석하기도 어렵기 때문에, 문제를 간단하게 하기 위해 stationary time signal이라 가정하고 분석하는 것으로 시작한다.

1) Stationary

$X_t$ is stationary if its joint distribution does not change

¹

- Strictly Stationary time series

$X_t$ is strictly stationary time series if
for CDF $F_{t_1, \cdots, t_n}(x_1, \cdots, x_n) = P(X_{t_1} \leq x_1, \cdots, X_{t_n} \leq x_n)$,
$F_{t_1, \cdots, t_n}(x_1, \cdots, x_n) = F_{t_1+h, \cdots, t_n+h}(x_1, \cdots, x_n)$ for all $n$ and $h > 0$

ex1) For $n=1, \ F_t(x) = P(X_t \leq x) = F_{t+h}(x)$
ex2) For $n=2, \ Cov(X_t, X_s) = Cov(X_{t+h}, X_{s+h})$

- (Weakly) Stationary time series

Strictly stationary 조건은 실질적으로 사용하기 어렵기 때문에 일반적으로 완화된 weakly stationary 조건을 사용한다.
$X_t$ is weakly stationary time series if
1) $E[X_t]$ is constant,
2) $Cov(X_t, X_s) = Cov(X_{t+h}, X_{s+h})$ for all $t, s$
    $Cov(X_t, X_{t+h})$ only depends on $h$ (not $t$)
3) $Var(X_t) = Var(X_{t+h})$

ex) White noise is stationary
1) $E[a_t] = 0$
2) $Cov(a_t, a_s) = Cov(a_{t+h}, a_{s+h}) = 0$
3) $Var(a_t) = Var(a_{t+h})$

- Autocovariance function

Autocovariance function of $X$: $\gamma_X(h) = Cov(X_t, X_{t+h})$

• $\gamma_X(h)$ only depends on $h$(lag)

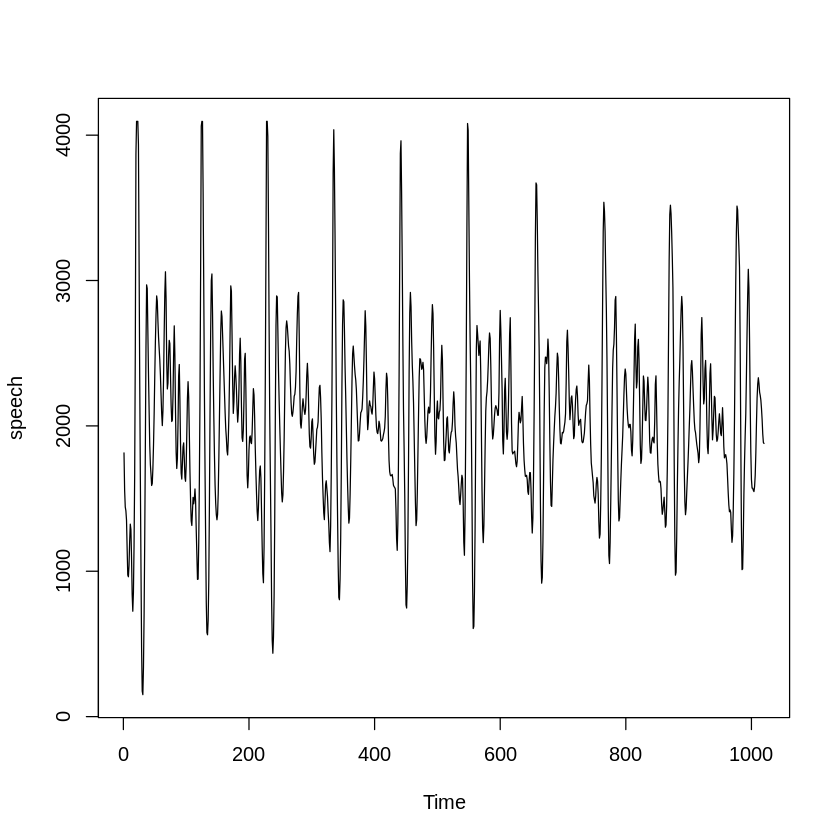
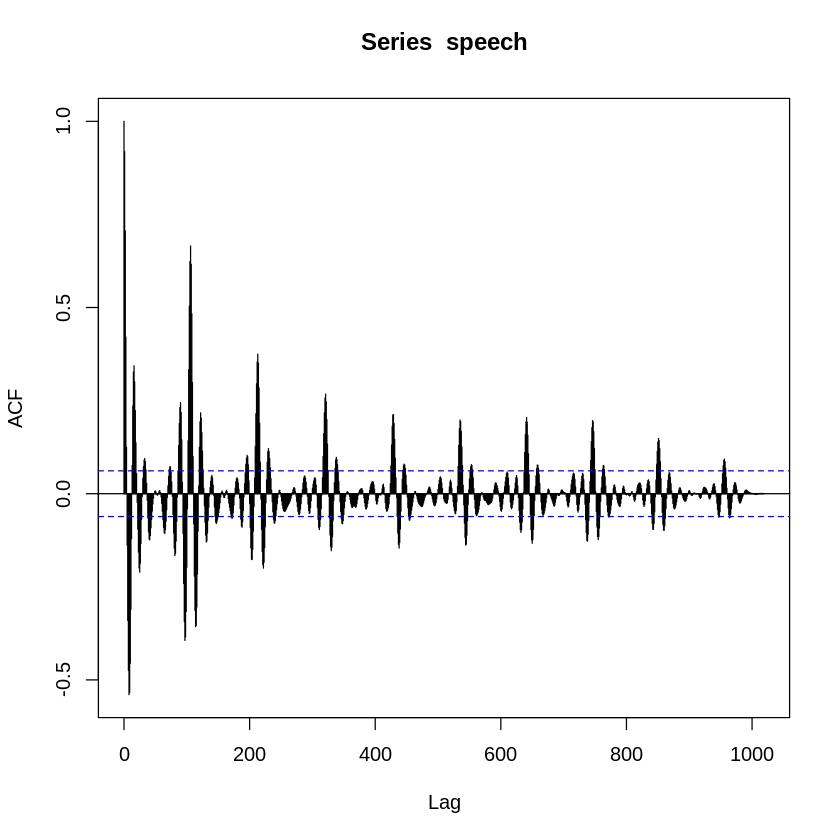
ex) speech dataset and ACF(AutoCovariance Function)

---