Alchemine Studio

3. Randomized Algorithm - Min-cut problem of a graph

 
  • Mar 25, 2020

Remarks

이 글은 인하대학교 최동완 교수님의 빅데이터컴퓨팅 수업을 정리한 자료입니다.

Remind

  • Graph Graph $G = (V, E)$   $V$: a set of vertices(nodes), $E$: a set of edges

  • Edge Parallel edges $e_1: (V_i, V_j), \ e_2: (V_i, V_j)$ Self loop edge $e: (V_i, V_i)$ Simple graph: A graph without parallel edges, self loop edges

  • Chain rule $\Pr[\cap_{i=1}^k E_i] = \Pr[E_1] \times \Pr[E_2 \mid E_1] \times \cdots \times \Pr[E_k \mid \cap_{i=1}^{k-1} E_i]$

I. Randomized min-cut algorithm (unweighted) (Karger algorithm)

1. Duality

Edge의 capacity를 최대화시키는 Max-flow problem의 dual problem에 해당한다.

2. Define problem

Input: Graph $G = (V, E)$ (connected and undirected multigraph(parallel edge 가능), $\mid V \mid = n, \mid E \mid = m$) Output: a set of edges, $E’ \subseteq E$ s.t.

  1. $E’$를 제거하면 $G$가 2개 이상의 graph로 나뉘어진다.
  2. 1의 조건을 만족하는 edge set 중에 $\mid E’ \mid$이 최소가 되어야 한다.

3. Algorithm of Randomized Min-cut

  1. Pick and edge uniformly at random, say $e \in E$.
  2. Merge the two end vertices $(V_i, V_j)$ into a new vertex $(V_{ij})$ retaining all edges except self loop edge. (Contraction)
  3. Repeat steps 1 & 2 until only two vertices are left.
  4. Return the set of edges between two remaining vertices.

이 algorithm은 결과값이 random하여 단번에 Min-cut edges를 찾아내는 것을 보장하지 않는다. 대신, 우리는 randomized algorithm의 대략적인 cost에 대해서 알아보는 것을 목표로 한다.

Q. How many removal steps are required?

1번 edge를 없앨 때마다 1개의 vertex가 합쳐진다. 2개의 vertex가 남을 때까지 edge를 제거하기 때문에 총 $n-2$번의 edge removal이 필요하다. 한 번의 removal은 merge(union) cost 등의 연산들이 필요하기 때문에 최소 $O(n)$ 이상의 cost가 소모된다. 따라서, $\Theta(n)$번의 removal step이 필요하고, 결국 $O(n^2)$의 복잡도를 가진다. 한편, 우리는 high level에 집중할 것이기 때문에 세부적인 구현에 대한 내용은 생략할 것이다.

4. Analysis of RandMC

1) What is the prob. of RandMD returning the optimal answer(min-cut)?

  1. Let $C \subseteq E$ be a min-cut s.t. $\mid C \mid = k$

  2. No vertex has degree smaller than $k$ (lemma1)

  3. $m \geq \frac{k \cdot n}{2}$ (lemma2)

  4. At the $i$’th step, let $\epsilon_i$ be an event of not picking on edge of $C$ $\Pr(\text{an edge of $C$ being selected}) = \frac{k}{m} \leq \frac{k}{kn_i/2} = \frac{2}{n_i} \quad (n_i: \text{# of vertices remained in $i$’th step})$ $\Pr(\epsilon_1) \geq 1 - \frac{2}{n}$ $\Pr(\epsilon_2 \mid \epsilon_1) \geq 1 - \frac{2}{n-1}$ $\Pr(\epsilon_i \mid \cap_{k=1}^{i-1} \epsilon_k) \geq 1 - \frac{2}{n_i} = \frac{2}{n - i + 1}$

  5. To find an optimal answer, $\Pr(\text{getting optimal answer}) \geq \Pr(\epsilon_1) \times \Pr(\epsilon_2 \mid \epsilon_1) \times \cdots \Pr(\epsilon_{n-2} \mid \cap_{i=1}^{n–3}\epsilon_i)$                 $\geq \Pi_{i=1}^{n-2} (1 - \frac{2}{n-i+1})$                 $= \Pi_{j=n}^3 (\frac{j-2}{j})$                 $= \frac{n-2}{n} \times \frac{n-3}{n-1} \times \frac{n-4}{n-2} \times \frac{n-5}{n-3} \times \cdots \times \frac{1}{3}$                 $= \frac{2}{n(n-1)}$                 $\approx \Omega(\frac{1}{n^2})$ : lower bound

2) Improve the complexity

  1. Probability of failure (getting non-optimal answer) $\Pr(\text{getting non-optimal answer}) \leq 1 - \frac{2}{n(n-1)} \leq 1 - \frac{2}{n^2}$

  2. Repeat $i$ times the same process of RandMC $\Pr(\text{getting non-optimal answers in every $i$ times}) \leq (1 - \frac{2}{n^2})^i$

  3. If $i = n^2$, then $\Pr(\text{getting non-optimal answers in every $i$ times}) \leq (1 - \frac{2}{n^2})^{n^2} = e^{-2} \approx 0.14$

  4. 즉, $O(n^4)$의 complexity를 고려한다면 약 14%의 정확도로 min-cut edges를 얻을 수 있다. 사실, deterministic algorithm의 경우 $O(n^3)$ 만으로 min-cut edges를 얻을 수 있다.

3) Boosting (the success probability): 중요!!

항상 $e^{-2}$라는 상수값에 성공확률이 bound되는 것이 아니라 $n$이 커질수록 좀 더 성공확률이 높아졌으면 좋겠다!

  1. Let us set $i = \frac{n^2}{2} \ln n$
  2. $\Pr(\text{getting non-optimal answer}) \leq (1 - \frac{2}{n^2})^{\frac{n^2}{2} \ln n} \approx \frac{1}{n}$
  3. $\Pr(\text{getting optimal answer}) \geq 1 - \frac{1}{n}$ Time: $O(n^4 \ln n)$
  • Boosting Let $p$ a success prob. of a given randomized algorithm. Then, let us run the algorithm $\frac{1}{p} \ln (\frac{1}{\delta})$ times, where $\delta$ is the target failure prob. The algorithm with $\frac{1}{p} \ln (\frac{1}{\delta})$ trials is correct with prob. at least $1 - \delta$ $\because \ \Pr(\text{failure}) = (1 - p)^{\frac{1}{p} \ln (\frac{1}{\delta})} = \delta$

II. Fast min-cut algorithm (a.k.a. Karger-Stein algorithm)

  • Time: $O(n^2 \log n)$ Success prob.: $\Omega(\frac{1}{\log n})$

1. Intuition

Contraction을 수행할수록 min-cut edges를 선택하지 않을 확률이 커진다. 즉, 정확한 답을 얻을 확률이 점점 작아지는데 최종적으론 $\frac{1}{3}$까지 떨어지게 된다. Trial을 좀 더 효율적으로 하기 위해 성공확률이 높은 초반(아직 contraction을 많이 수행하지 않은 경우)에는 trial을 적게하고, 성공확률이 떨어지는 나중에는 더 많이 trial한다. 즉, graph의 size를 고려하여 boosting을 수행하는 방법이다.

2. Algorithm of Fast MC: 중요!! (왜 $\frac{1}{\sqrt{2}}$ 인가? 확률이 $\frac{1}{2}$ 로 줄어들기 때문에!)

  1. $n ← \mid V \mid$
  2. if $n < \lceil 2 \sqrt{2} + 1 \rceil$ then compute a min-cut by brute-force in $O(1)$ times 2.1. Contract $G$ until $\lceil \frac{n}{\sqrt{2} + 1} \rceil$ nodes remain → $G’$ 2.2. Perform Faster MC at $G’$ independently twice to obtain two resulting cuts, say $c_1$ and $c_2$ 2.3. Return the smaller of $c_1$ and $c_2$

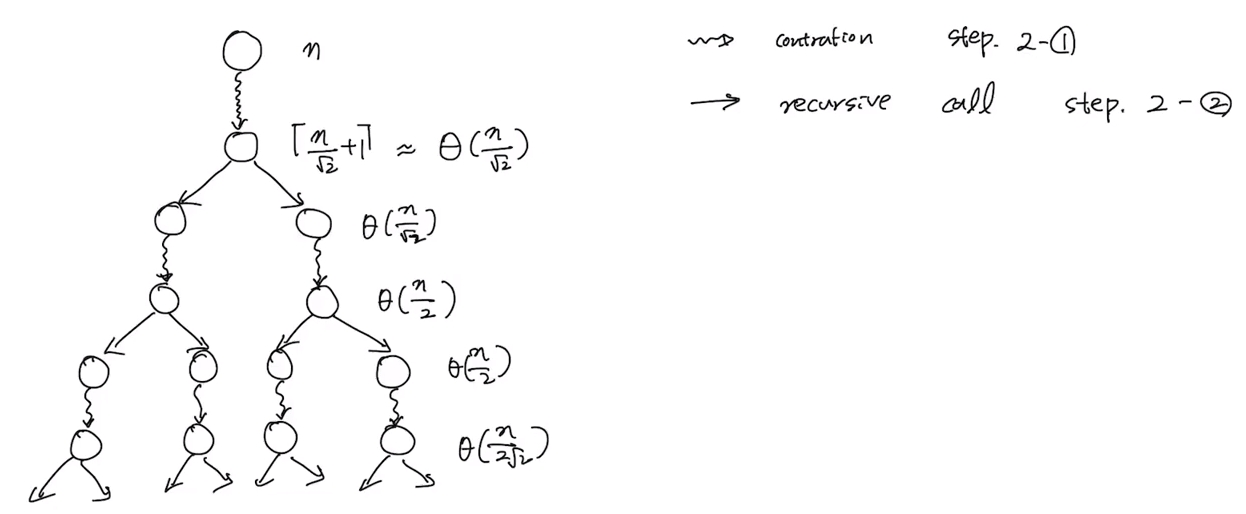
3. Algorithm analysis

1) Recursion depth

  1. Set $n_i = \text{# of vertices when $i$’th cut}$
  2. $n_1 = \Theta(\frac{n}{\sqrt{2}})$ $n_2 = \Theta(\frac{n}{\sqrt{2}^2})$ $n_i = \Theta(\frac{n}{\sqrt{2}^i})$
  3. $n_i \approx \frac{n}{\sqrt{2}^i} < 2\sqrt{2} + 1$ $\sqrt{2}^i > \frac{n}{2\sqrt{2} + 1}$ $i > \log_{\sqrt{2}} \frac{n}{2\sqrt{2} + 1}$    $= \log_{\sqrt{2}} n - \log_{\sqrt{2}}{2\sqrt{2} + 1}$    $= \log_2 n^2 - 2$    $= 2\log_2 n - 2$
  4. Recursion depth $i \approx \Theta(\log n)$

2) Number of leaf nodes

Number of leaf nodes: $2^i = 2^{\log_2 n^2 - 2} = \frac{n^2}{4} \approx \Theta(n^2)$ 동일한 횟수($\Theta(n^2)$)만큼 parallel하게 수행하는 것보다 훨씬 효율적이다.

4) Prob. of success of Faster MC

(lemma) Theprob. of a min-cut being alive until when $t$ vertices remain $\Pi_{i=1}^{n-t} (1 - \frac{2}{n-i+1}) = \Pi_{j=n}^{t+1}(\frac{j-2}{j}) = \cdots = \frac{t(t-1)}{n(n-1)} \approx \Omega(\frac{t^2}{n^2})$

  1. $\Pr[\text{Alive after 1st cutting}] = \frac{(\frac{n}{\sqrt{2}} + 1) \frac{n}{\sqrt{2}}}{n(n-1)}$   $(t_1: \frac{n}{\sqrt{2}} + 1)$                 $= \frac{(\frac{n}{\sqrt{2}} + 1) \frac{1}{\sqrt{2}}}{n-1}$                 $> \frac{(\frac{n}{\sqrt{2}} - \frac{1}{\sqrt2}) \frac{1}{\sqrt{2}}}{n-1}$                 $= \frac{(n-1) \frac{1}{2}}{n-1}$                 $= \frac{1}{2}$ $\therefore \ \Pr[\text{Alive after 1st cutting}] > \frac{1}{2}$
  2. Set $p(n)$ success probability of Faster MC with $n$ vertices
  3. $p(n) = 1 - \Pr(\text{Fail at left}) \times \Pr(\text{Fail at right})$     $= 1 - (1 - \Pr(\text{Success at left})) \times (1 - \Pr(\text{Success at right}))$
  4. $\Pr(\text{Success at left}) = Pr(\text{Success at right})$ $= \Pr(\text{Alive after 1st cutting}) \times p(\frac{n}{\sqrt2}) > \frac{1}{2} \times p(\frac{n}{\sqrt2})$ $\therefore \ \Pr(\text{Success at left}) > \frac{1}{2} \ p(\frac{n}{\sqrt2})$
  5. $p(n) > 1 - (1 - \frac{1}{2} \ p(\frac{n}{\sqrt2}))^2$     $> 1 - (1 - p(\frac{n}{\sqrt2}) + \frac{1}{4} \ p(\frac{n}{\sqrt2})^2)$     $= p(\frac{n}{\sqrt2}) - \frac{1}{4} \ p(\frac{n}{\sqrt2})^2$ $\therefore \ p(n) \approx p(\frac{n}{\sqrt2}) - \frac{1}{4} \ p(\frac{n}{\sqrt2})^2$
  6. Let $p_k$ success prob. of Faster MC at height $k$ ($=$ means $\approx$) $p_0 = 1, \ p_k = p_{k-1} - \frac{p_{k-1}^2}{4}$ $p_{k+1} = p_k - \frac{p_k^2}{4}$
  7. Let $q_k = \frac{4}{p_k} - 1, \ p_k = \frac{4}{q_k + 1} \approx \Theta(\frac{1}{q_k})$
  8. 6 becomes below $\frac{4}{q_{k+1} + 1} = \frac{4}{q_{k} + 1} - \frac{1}{4} (\frac{4}{q_{k} + 1})^2$ $\frac{1}{q_{k+1} + 1} = \frac{1}{q_{k} + 1} - \frac{1}{(q_{k}+1)^2}$     $= \frac{q_k}{(q_{k}+1)^2}$ $q_{k+1} = q_k + 1 + \frac{1}{q_k} > q_k + 1$
  9. Let $\hat q_{k+1} = \hat q_k + 1, \ \hat q_k = 3 + k \ (\because \ \hat q_0 = q_0 = 3)$ $q_{k+1} > \hat q_{k+1} = 4 + k$ $\frac{1}{q_k} < \frac{1}{k}$ $\therefore \ q_{k+1} = q_k + 1 + \frac{1}{q_k} < q_k + 1 + \frac{1}{k}$              $< q_{k-1} + (1 + 1) + (\frac{1}{k} + \frac{1}{k-1})$               $\vdots$              $< q_1 + k + \sum_{j=1}^k\frac{1}{j}$              $= 4 + k + \sum_{j=1}^k\frac{1}{j}$              $\approx 4 + k + (\ln k + \Theta(1))$              $\approx k + \ln k + C$
  10. $4 + k < q_{k+1} < k + \ln k + C$ $\frac{1}{k} > \frac{1}{q_k} > \frac{1}{k + \ln k}$
  11. $p_k \approx \Theta(\frac{1}{k}) \ (\because \ p_k \approx \Theta(\frac{1}{q_k}))$
  12. b.t.w. $k$ means height $\Theta(\log n)$ $p_k \approx \Theta(\frac{1}{\log n})$ In fact, $p_k > \Theta(\frac{1}{\log n})$ $\therefore \ p_k \approx \Omega(\frac{1}{\log n})$

5) Time complexity of Faster MC

$T(n) = O(n^2) + 2T(\frac{n}{\sqrt2})$