Remarks
이 글은 파이썬으로 배우는 포트폴리오을 정리한 자료입니다.
평균-분산 포트폴리오 이론의 가정
- 모든 투자자의 투자 기간은 1 기간이다.
- 투자자는 위험을 회피하고, 기대효용을 극대화하려 한다.
- 기대수익률과 표준편차에 따라 투자를 결정하며, 지배원리에 따라 투자 대상을 선택한다.
- 거래비용과 세금은 없으며, 모든 투자자는 무위험이자율로 한도 없는 차입과 대출을 할 수 있다.
3.1 포트폴리오의 기대수익률과 위험
https://thebook.io/080227/ch03/01/
포트폴리오(portfolio)
여러 개의 투자 대상을 모은 집합
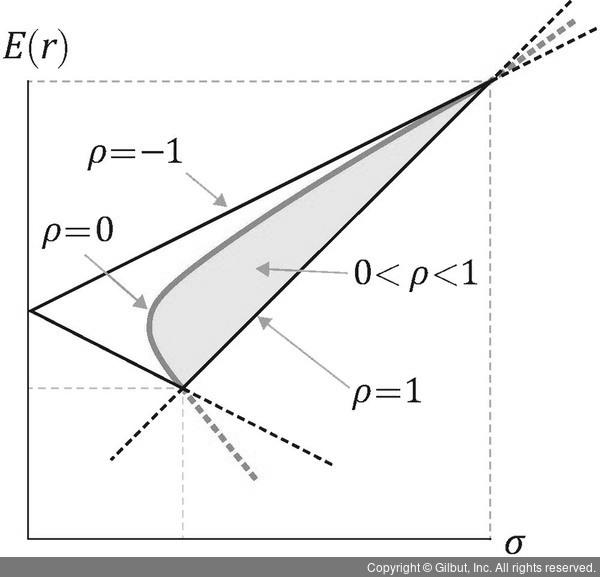
- 두 자산의 상관계수가 0에 가까울수록 투자기회집합선은 왼쪽으로 휘어진다.
즉, 분산 투자의 효과를 통해 위험을 줄일 수 있다. - 평균-분산 포트폴리오 이론에서 제시하는 최적 포트폴리오를 구하는 간략한 과정
포트폴리오 수익률의 기대수익률과 리스크를 계산하고 지배원리에 따라 포트폴리오를 걸러낸다.
그리고 무차별곡선을 이용해 최적 포트폴리오를 결정한다.
포트폴리오의 기대수익률
$E[r_p] = \sum_i w_i E[r_i] = W’R$
- $W$: 자산의 투자 비중 $([n, 1])$
- $R$: 자산의 기대수익률 $([n, 1])$
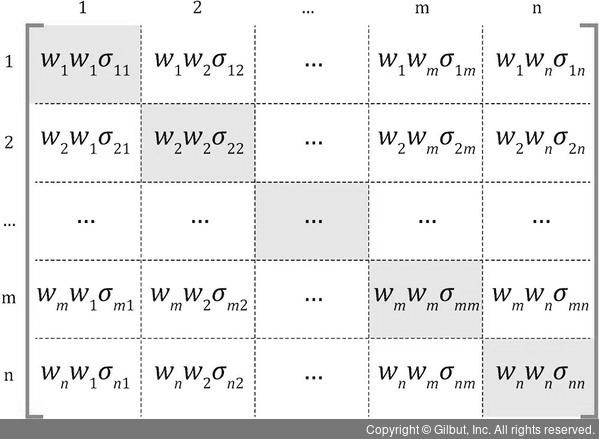
포트폴리오의 위험
$\sigma_p^2 = \sum_i \sum_j w_i w_j \sigma_{ij} = \sum_i w_i^2 \sigma_i^2 + \sum_i \sum_{j \neq i} w_i w_j \rho_{ij} \sigma_i \sigma_j = W’\Sigma W$
- $W$: 자산의 투자 비중 $([n, 1])$
- $\Sigma$: 자산 수익률에 대한 공분산 행렬 $([n, n])$
- $\rho_{ij}$: 자산 $i$와 $j$간의 상관계수 $(\rho_{ij} = \frac{\sigma_{ij}}{\sigma_i \sigma_j})$
https://thebook.io/080227/ch03/01/02-07/
3.2 최소분산포트폴리오
분산 효과(포트폴리오 효과)
포트폴리오를 구성함으로써 같은 기대수익률하에 위험이 줄어드는 효과
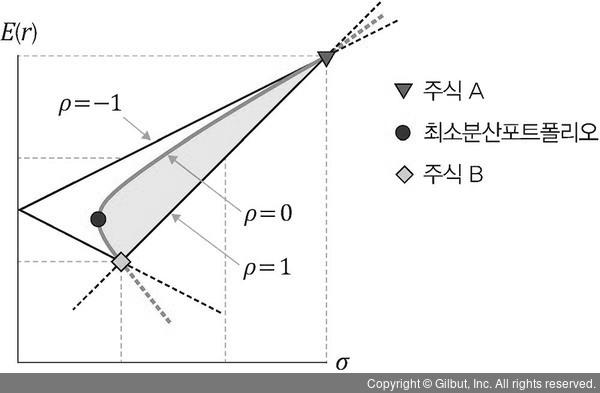
최소분산포트폴리오(Minimum Variance Portfolio, MVP)
자산 간의 상관계수가 0인 경우, 가장 위험이 적은 투자 비중 조합을 가진 포트폴리오
https://thebook.io/080227/ch03/02/
- 주식 A와 B에 대한 투자 비중은 다음 공식을 통해 구할 수 있다.
$w_A = \frac{\sigma_B^2 - \sigma_{AB}}{\sigma_A^2 + \sigma_B^2 - 2\sigma_{AB}}$
$w_B = 1 - w_A$
실전 예제
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
from pykrx import stock
from datetime import datetime
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.DataFrame()
dates = pd.date_range(start='2022-01-01', end='2022-02-01').strftime("%Y%m%d")
for date in dates:
df_cur = df.append(stock.get_market_ohlcv_by_ticker(date=date, market='KOSPI'))
if (df_cur == 0).all(None):
continue
df_cur['날짜'] = date
df_cur = df_cur[['날짜', '등락률']]
df = df.append(df_cur)
df = df.pivot_table(index='날짜', columns='티커', values='등락률')
df
티커 000020 000040 000050 000060 000070 000075 000080 000087 000100 000105 ... 383220 383800 38380K 395400 396690 400760 402340 404990 900140 950210
날짜
20220103 2.400000 1.270000 0.000000 2.830000 -0.920000 -0.580000 0.330000 1.050000 2.090000 1.020000 ... 0.000000 1.500000 1.640000 0.970000 -1.080000 0.190000 0.150000 -0.400000 1.240000 2.160000
20220104 1.035000 1.950000 1.090000 5.255000 0.155000 -0.580000 0.250000 -0.510000 0.100000 0.510000 ... -1.375000 2.230000 2.440000 -0.080000 -0.540000 0.000000 2.705000 -0.150000 0.415000 0.375000
20220105 0.530000 1.792500 0.635000 4.142500 -0.330000 -0.435000 -0.122500 0.272500 0.130000 0.217500 ... -0.960000 1.370000 1.160000 0.242500 -0.630000 0.047500 0.532500 -0.250000 0.312500 0.072500
20220106 0.566250 1.378750 0.633750 3.363750 -0.612500 -0.508750 0.272500 0.107500 0.146250 0.385000 ... -1.318750 1.250000 1.235000 0.182500 -0.631250 -0.001250 -0.130000 -0.187500 0.277500 0.033750
20220107 0.848750 1.467500 0.611875 4.021875 -0.367500 -0.499375 0.219375 0.123750 0.321250 0.374375 ... -0.820625 1.370625 1.335000 0.253125 -0.608125 0.023125 0.345000 -0.206250 0.424375 0.248125
20220108 0.771875 1.464063 0.611875 3.786562 -0.397188 -0.485625 0.188438 0.123750 0.285000 0.374375 ... -0.945938 1.355312 1.325000 0.227813 -0.608125 0.023125 0.380313 -0.203125 0.385312 0.232500
20220109 0.771875 1.464063 0.611875 3.786562 -0.397188 -0.485625 0.188438 0.123750 0.285000 0.374375 ... -0.945938 1.355312 1.325000 0.227813 -0.608125 0.023125 0.380313 -0.203125 0.385312 0.232500
20220110 0.771875 1.431328 0.617422 3.836406 -0.401250 -0.489062 0.183359 0.117578 0.281172 0.373047 ... -0.982109 1.362891 1.327500 0.217734 -0.611016 0.020078 0.335469 -0.210156 0.363906 0.210938
20220111 0.765195 1.445000 0.616016 3.822969 -0.402070 -0.485586 0.183359 0.118594 0.288906 0.389609 ... -0.957266 1.355352 1.326250 0.221484 -0.613164 0.023867 0.355859 -0.207422 0.371289 0.211641
20220112 0.768535 1.447930 0.617383 3.828145 -0.397539 -0.482695 0.189453 0.121699 0.288867 0.377207 ... -0.959316 1.356269 1.324375 0.223086 -0.611367 0.022734 0.364395 -0.207832 0.375996 0.220293
20220113 0.766836 1.447139 0.616699 3.826279 -0.399697 -0.484150 0.188145 0.121182 0.286494 0.376992 ... -0.957666 1.356269 1.324043 0.222451 -0.611182 0.022168 0.358330 -0.207832 0.374746 0.216201
20220114 0.766821 1.447139 0.617031 3.822598 -0.400215 -0.485215 0.186738 0.120669 0.286411 0.378130 ... -0.958823 1.356269 1.323716 0.222529 -0.611455 0.022070 0.360322 -0.207632 0.373521 0.216563
20220115 0.767254 1.447139 0.616780 3.823540 -0.399805 -0.484790 0.187166 0.120796 0.286687 0.378171 ... -0.958823 1.356389 1.324197 0.222529 -0.611365 0.022261 0.359902 -0.207632 0.374065 0.216953
20220116 0.767254 1.447139 0.616780 3.823540 -0.399805 -0.484790 0.187166 0.120796 0.286687 0.378171 ... -0.958823 1.356389 1.324197 0.222529 -0.611365 0.022261 0.359902 -0.207632 0.374065 0.216953
20220117 0.767033 1.446949 0.616780 3.823679 -0.399987 -0.484907 0.187047 0.120715 0.286627 0.378109 ... -0.959025 1.356299 1.324176 0.222539 -0.611422 0.022201 0.359934 -0.207738 0.373890 0.216821
20220118 0.767075 1.447015 0.616769 3.823739 -0.399929 -0.484839 0.187091 0.120756 0.286642 0.378124 ... -0.958900 1.356359 1.324125 0.222539 -0.611393 0.022237 0.360103 -0.207679 0.373982 0.216794
20220119 0.767056 1.447004 0.616780 3.823719 -0.399897 -0.484855 0.187091 0.120756 0.286634 0.378127 ... -0.958924 1.356352 1.324156 0.222529 -0.611399 0.022240 0.359996 -0.207682 0.373978 0.216776
20220120 0.767095 1.447017 0.616780 3.823704 -0.399898 -0.484844 0.187103 0.120758 0.286644 0.378131 ... -0.958900 1.356348 1.324158 0.222532 -0.611392 0.022243 0.360006 -0.207684 0.373990 0.216838
18 rows × 942 columns
1
2
3
4
n = 10
codes = np.random.choice(df.columns, n)
corr = df[codes].corr()
sns.heatmap(np.triu(corr.loc[codes, codes], k=1), cmap='coolwarm', center=0, annot=True);
.png)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
pair_pos = df[codes].columns[[3, 8]]
pair_zero = df[codes].columns[[2, 6]]
pair_neg = df[codes].columns[[4, 8]]
def exp_return(r1, r2, w1):
exp_r1 = r1.mean()
exp_r2 = r2.mean()
return w1*exp_r1 + (1-w1)*exp_r2
def risk(r1, r2, w1):
var1 = r1.var(ddof=1)
var2 = r2.var(ddof=1)
cov = np.cov(r1, r2, ddof=1)[0, 1]
return np.sqrt(w1**2 * var1 + (1-w1)**2 * var2 + 2*w1*(1-w1)*cov)
def mv_plot(df, pair, ax):
A, B = pair
r_A, r_B = df[A].values, df[B].values
for w in np.arange(0, 1, 0.01):
X, y = risk(r_A, r_B, w), exp_return(r_A, r_B, w)
ax.plot(X, y, '.')
ax.set_xlabel('risk'), ax.set_ylabel('expected return')
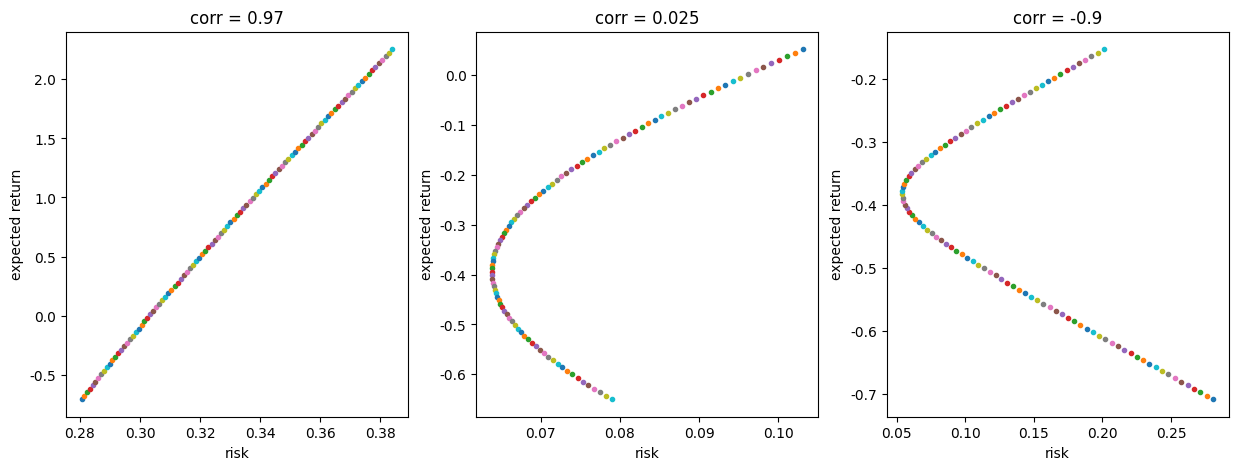
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
for ax, pair, title in zip(axes, [pair_pos, pair_zero, pair_neg], ['corr = 0.97', 'corr = 0.025', 'corr = -0.9']):
mv_plot(df, pair, ax)
ax.set_title(title)
3.3 체계적 위험과 비체계적 위험
위험의 구분
\1. 체계적 위험(systematic risk, market risk): 모든 기업에 공통적으로 영향을 미치는 요인에 의해 발생하는 위험 (분산 투자로 제거 불가능)
- 경제변수(이자율, 환율, 경기선행지수, 실업률, 경제정책 등)의 불리한 움직임
\2. 비체계적 위험(unsystematic risk): 특정 기업에 의해 발생하는 위험 (분산 투자로 제거 가능)
- 개별 주식과 관련된 고유의 위험(어닝쇼크(실적 부진), 소송, 노사분규 등)
3.3.1 체계적 위험의 측정
- 체계적 위험은 주식시장 전체 변동에 대한 개별 종목의 변동 정도로 측정
- 구체적으론, 주식시장 전체 변화율과 개별 종목 변화율 간 회귀방정식의 기울기(베타, $\beta$)를 의미
3.3.2 구성 종목수가 많을수록 개별 종목의 분산은 무의미해진다
\(\begin{equation} \begin{aligned} \sigma_p^2 &= \sum_i \sum_j w_i w_j \sigma_i \sigma_j \\ &= \sum_i w_i^2 \sigma_i^2 + \sum_i \sum_{i \neq j} w_i w_j \sigma_{ij} \\ &= \sum_i (\frac{1}{n})^2 \sigma_i^2 + \sum_i \sum_{i \neq j} (\frac{1}{n})^2 \sigma_{ij} \quad \cdots \quad \forall_i w_i = \frac{1}{n} \\ &= \frac{1}{n} \sum_i \frac{1}{n} \sigma_i^2 + \frac{n-1}{n} \sum_i \sum_{i \neq j} \frac{1}{n(n-1)} \sigma_{ij} \\ &= \frac{1}{n} \bar \sigma_i^2 + (1 - \frac{1}{n}) \bar \sigma_{ij} \\ &= \frac{1}{n}(\bar \sigma_i^2 - \bar \sigma_{ij}) + \bar \sigma_{ij} \\ &= \bar \sigma_{ij} \quad \cdots \quad \lim n \rarr \infty \end{aligned} \end{equation}\)
- 포트폴리오의 위험은 각 종목의 분산과 종목간의 공분산으로 구성됨
- 동일 가중치 포트폴리오를 구성하는 경우,
종목의 개수를 늘릴수록 개별 종목의 분산은 의미를 잃고 종목 간 공분산만이 포트폴리오의 위험을 나타냄
3.4 무위험자산과 최적 자산배분
무위험자산(risk-free asset)
이자율, 인플레이션 변화에도 영향을 받지 않아 미래의 현금흐름에 불확실성이 없는 자산