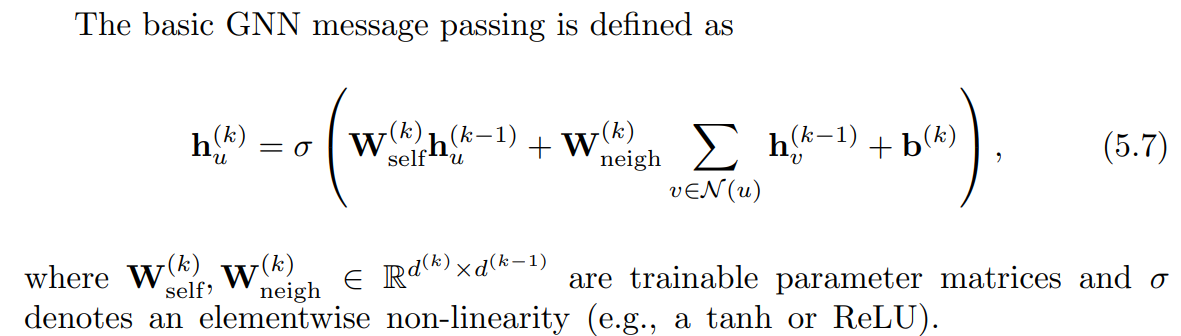Alchemine Studio

Graph Neural Network

 
  • Sep 08, 2023

Remarks

120. Graph Neural Network(GNN)의 정의부터 응용까지 (한국원자력연구원 인공지능응용전략실 최희선 선임연구원), [논문 리뷰] Graph Neural Networks (GCN, GraphSAGE, GAT) - 김보민 등의 내용을 정리한 글입니다.

1. Introduction to Graph Neural Networks

1.1 Graph representation learning

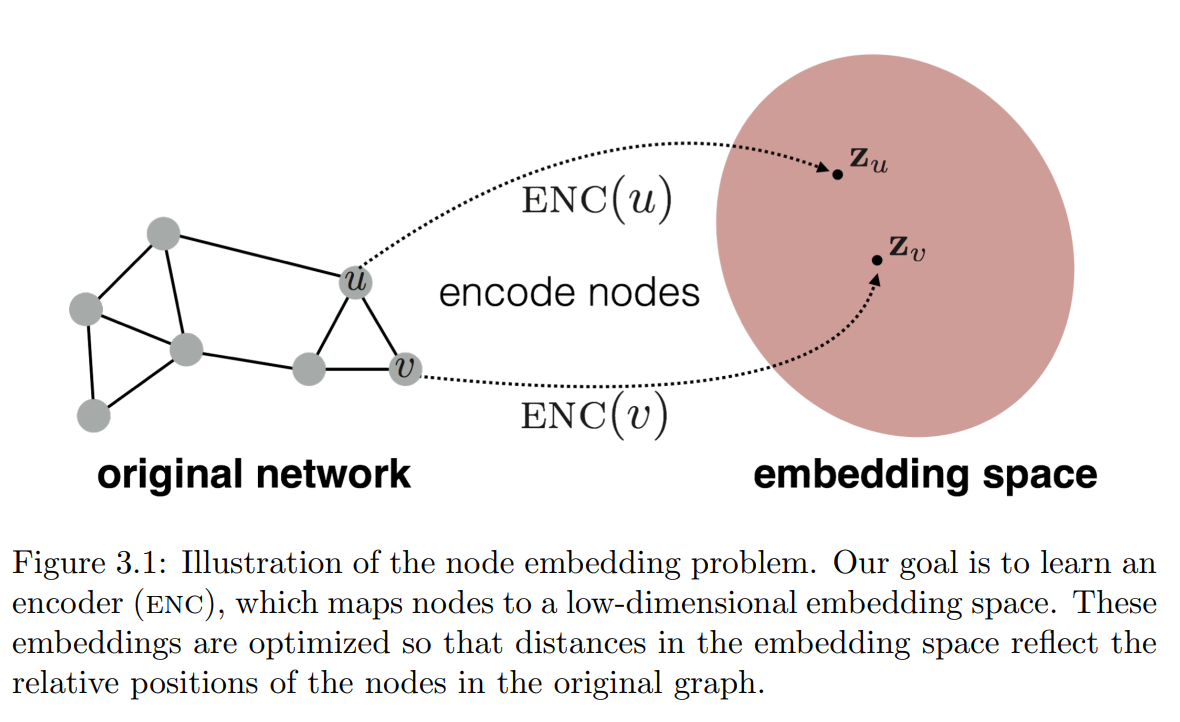
Graph representation learning
Summarizing the structure of a graph in a low dimensional space(embedding space)

Alt text1

1.2 Node embedding

1.2.1 Shallow embedding method

General embedding like NLP

  1. One-hot encoding nodes
  2. Embed with matrix (embedder, shape: [#emb_dim, #nodes])
  3. How to learning embedder
    1. Measure smilarity between nodes: $S(A, C)$
    2. Optimize the parameters of the embedder to preserve the similarity
      $S(A, C) \approx S(E(A), E(C))$
  4. Inherent issues
    1. The size of an embedder increases linearly with the number of nodes
    2. Difficult in defining the similarity metric
  5. Example
    Node2Vec, DeepWalk, LINE, …
    • Node2Vec performs good if don’t matter the embedder size

1.2.2 Neural network-based methods

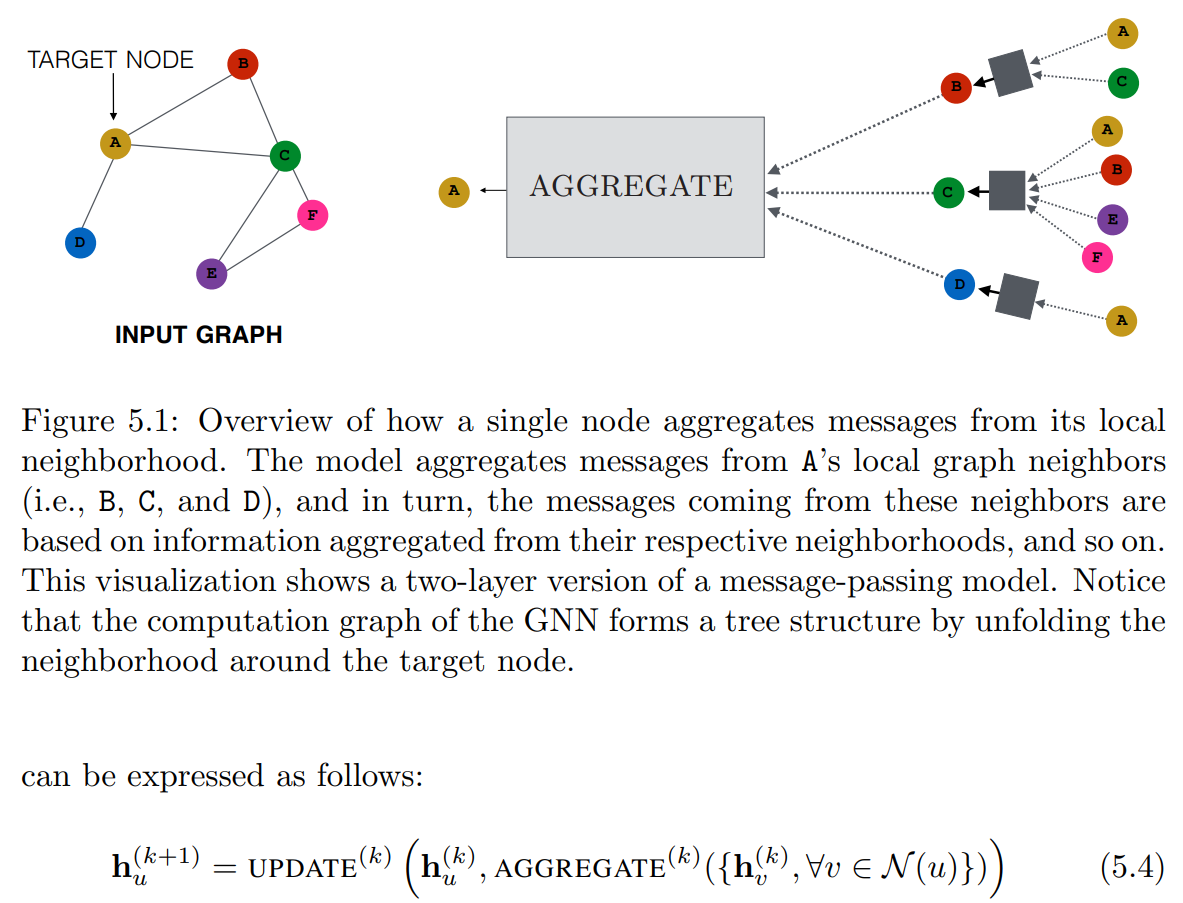
  1. Message passing GNN
    • Concept: a node is represented with the neighbors(context)

Alt text1 Alt text1

  • UPDATE, AGGREGATE: arbitrary differentiable functions (e.g. NN)
  1. Weisfeiler-Lehman GNNs
    pass

1.3 Notation

Given a graph $G$:

  • $V$: set of vertices
  • $A$: binary adjacency matrix
  • $X \in R^{m \times \mid V \mid}$: a matrix of node features

1.4 Graph tasks

  1. Node classification
    Categorize users/items
  2. Link prediction
    Grpah completion
  3. Graph classification
    Molecule property prediction
  4. Clustering
    Social circle detection
  5. Graph generation
    Drug discovery

2. Graph Convolution Networks (GCN, ICLR 2017)

Kipf, Thomas N., and Max Welling. “Semi-supervised classification with graph convolutional networks.” arXiv preprint arXiv:1609.02907 (2016).

2.1 CNN vs GCN

  • CNN: Spatial location(euclidean distance) based
  • GCN: Neighborhood(edge) based

2.2 Concept

Theoretical point of view: “Neighborhood Normalization”

  • Aggregation without normalization (previous)
    $\sum_{v \in \mathcal{N}(u)} h_v$: unstable and highly sensitive to node degrees
  • Use symmetric normalization aggregation function (proposed)
    $\sum_{v \in \mathcal{N}(u)} h_v \rarr \sum_{v \in \mathcal{N}(u)} \frac{h_v}{\sqrt{ \mid \mathcal{N}(u) \mid \mid \mathcal{N}(v) \mid }}$

2.3 Learning node embeddings: iterative method

2.3.1 GCN layer

$H^{(l+1)} = \sigma(\tilde D^{-1/2} \tilde A \tilde D^{-1/2} \ H^{(l)} W^{(l)})$
$H^{(l+1)} = \sigma(\quad \quad \ \ \hat A \ \ \ \quad\quad H^{(l)} W^{(l)})$
$\sigma: \text{ReLU}$

  1. $H^{(l)} \in R^{N \times D}$: matrix of activations in the $l$-th layer
  2. $\tilde A = A + I_N$: adjacency matrix + self-connections
    $\tilde D_{ii} = \sum_j \tilde A_{ij}$: diagonal matrix
  3. $\hat A = \tilde D^{-1/2} \tilde A \tilde D^{-1/2}$: normalized adjacency matrix (preprocessing)
    Smaller degree${i}$ → bigger $A’{ii}$
  4. $H^{(0)} = X$
  5. $\hat A H^{(l)}$: aggregation(linear combination of node feature2)
    $i$-th row: weighted sum of adjacent node features of $i$-th node

ex) 2-layer GCN (classification)

  1. Preprocessing
    $\hat A = \tilde D^{-1/2} \tilde A \tilde D^{-1/2}$
  2. Forward
    $Z_1 \ \ = \quad \quad \quad \quad \text{ReLU} (\hat A X W^{(0)})$
    $Z_{out} = \text{softmax}(\text{ReLU} (\hat A Z_1 W^{(1)}))$
  3. Loss function(CEE)
    $L = \sum_l \sum_f y_{lf} \ln Z_{lf}$

2.4 Key factors

  1. Definition of neighborhood
    • Distance
    • Adjacency matrix
  2. How to aggregate
    • Attention and Edge weights
    • (Neighborhood) Normalization
    • Ordering of nodes (cf. check permutation invariance / equivalence)

2.5 Deep Graph Library(DGL)

DEEP GRAPH LIBRARY: Easy Deep Learning on Graphs

from torch import nn
import torch.nn.functional as F
from dgl.nn import GraphConv


class GCN(nn.Module):
    def __init__(self, in_feats, h_feats, num_classes):
        super(GCN, self).__init__()
        self.conv1 = GraphConv(in_feats, h_feats)
        self.conv2 = GraphConv(h_feats, num_classes)

    def forward(self, g, in_feat):
        h = self.conv1(g, in_feat)
        h = F.relu(h)
        h = self.conv2(g, h)
        return h

3. GraphSAGE (NeurIPS 2017)

Hamilton, Will, Zhitao Ying, and Jure Leskovec. “Inductive representation learning on large graphs.” Advances in neural information processing systems 30 (2017).

3.1 GCN → GraphSAGE

  • GraphSAGE
    Generating embeddings by SAmpling and AGgregating features from a node’s local neighborhood

Alt text

  • AGGREGATE
    • GraphSAGE-GCN: $\text{AGGREGATE}$ = weighted sum
    • GraphSAGE-mean: $\text{AGGREGATE}$ = mean
    • GraphSAGE-LSTM: $\text{AGGREGATE}$ = LSTM (high cost but not good)
    • GraphSAGE-pool: $\text{AGGREGATE}$ = pool

3.2 Deep Graph Library(DGL)

from torch import nn
import torch.nn.functional as F
from dgl.nn import SAGEConv


class GCN(nn.Module):
    def __init__(self, in_feats, h_feats, num_classes):
        super(GCN, self).__init__()
        self.conv1 = SAGEConv(in_feats, h_feats, 'mean')
        self.conv2 = SAGEConv(h_feats, num_classes, 'mean')

    def forward(self, g, in_feat):
        h = self.conv1(g, in_feat)
        h = F.relu(h)
        h = self.conv2(g, h)
        return h

4. Graph Attention Networks (GAT, ICLR 2018)

Veličković, Petar, et al. “Graph attention networks.” arXiv preprint arXiv:1710.10903 (2017).

4.1 GNN applied Attention

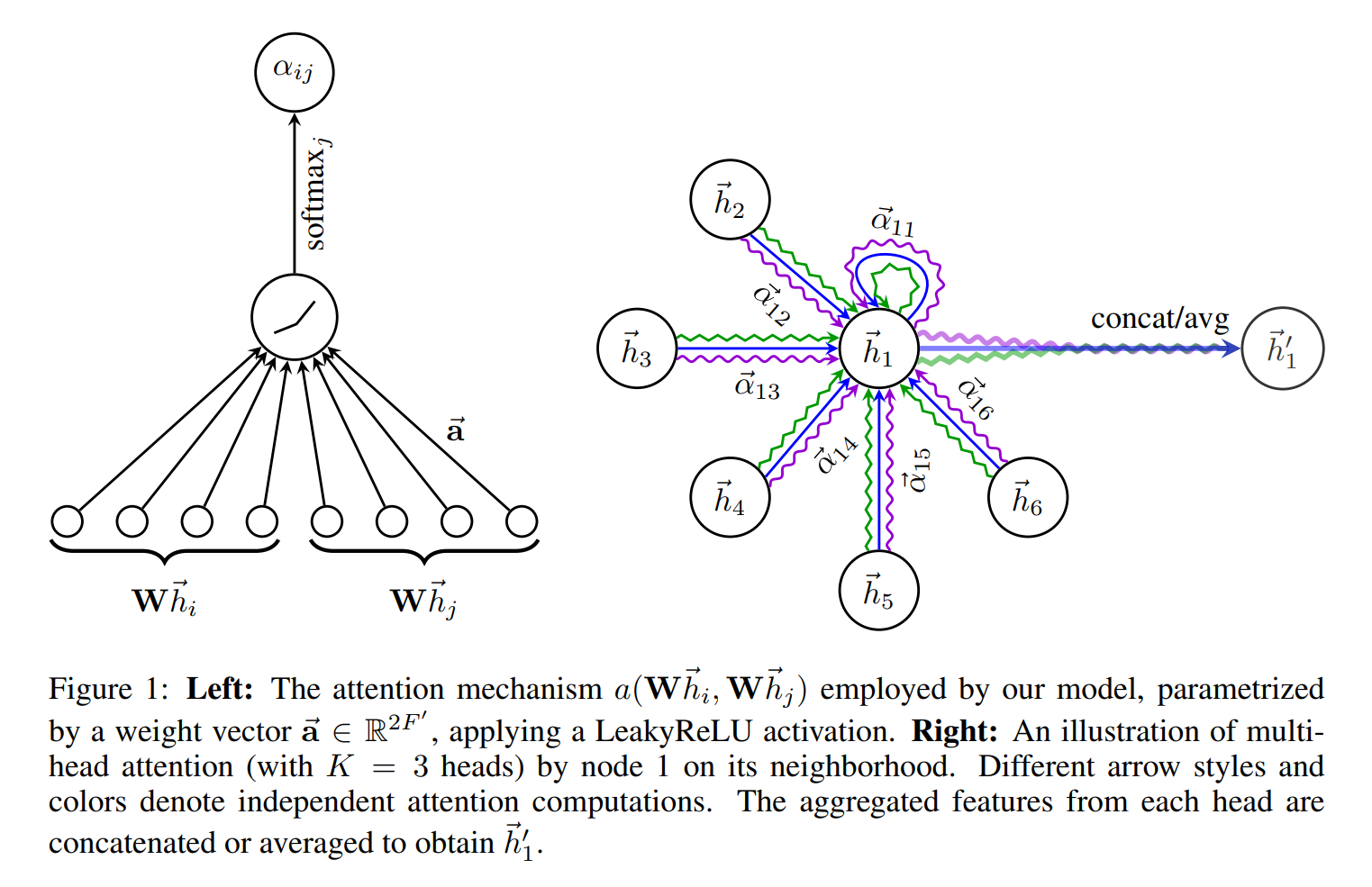
Alt text

  1. Attention components
    1. Query: $h_j \in R^{F}$
    2. Key, value: $h_i \in R^{F}$
    3. Masked if not neighbors of $j$’th node
    4. Projection matrix: $W \in R^{F’ \times F}$
  2. Attention algorithm
    1. Transform input features($F$) into high-level features($F’$)
      1. Query: $h_j \rarr Wh_j$
      2. Key: $h_i \rarr Wh_i$
    2. Compute attention coefficients
      • Attention mechanism $a: R^{2F’} \rarr R$
        • Single-layer FC with LeakyReLU - $2F’$: concatenated query($F’$) and key($F’$)
      • Compute attention coefficient
        $e_{ij} = a(Wh_i, Wh_j)$
    3. Normalize attention coefficient
      $\alpha_{ij} = \text{softmax}j(e{ij})$
    4. Compute a linear combination of the features
      $h’_i = \sigma(\sum_j \alpha_j Wh_j)$

    5. Employ multi-head attention to stabilize the learning process
      $h’^k_i = \sigma(\sum_j \alpha^k_j W^kh_j)$
      $h’_i = \text{concat}_k(h’^k_i)$

      • On final(prediction) layer
        $h’_i = \sigma(\text{mean}_k(\sum_j \alpha^k_j W^kh_j))$
        • Employ averaging instead of concatenation
        • Delay applying nonlinarity

4.2 Deep Graph Library(DGL)

from torch import nn
import torch.nn.functional as F
from dgl.nn import GATConv
 

class GAT(nn.Module):
    def __init__(self, insize, hid_size, out_size, heads):
        super().__init__()
        self.conv1 = GATConv(in_size, hid_size, heads[0], feat_drop=0.6, attn_drop=0.6, activation=F.elu)
        self.conv2 = GATConv(hid_size*heads[0], out_size, heads[1], feat_drop=0.6, attn_drop=0.6, activation=None)

    def forward(self, g, inputs):
        h = self.conv1(g, inputs)
		h = h.flatten(1)
        h = self.conv2(g, h)
		h = h.mean(1)
        return h

References

  1. Graph Representation Learning ↩ ↩2 ↩3

  2. Elementary row operation ↩